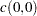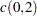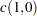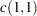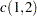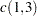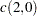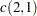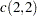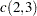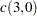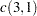| The ARIMA Procedure |
| The SCAN Method |
The smallest canonical (SCAN) correlation method can tentatively identify the orders of a stationary or nonstationary ARMA process. Tsay and Tiao (1985) proposed the technique, and Box, Jenkins, and Reinsel (1994) and Choi (1992) provide useful descriptions of the algorithm.
Given a stationary or nonstationary time series  with mean corrected form
with mean corrected form 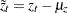 with a true autoregressive order of
with a true autoregressive order of 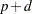 and with a true moving-average order of
and with a true moving-average order of  , you can use the SCAN method to analyze eigenvalues of the correlation matrix of the ARMA process. The following paragraphs provide a brief description of the algorithm.
, you can use the SCAN method to analyze eigenvalues of the correlation matrix of the ARMA process. The following paragraphs provide a brief description of the algorithm.
For autoregressive test order  and for moving-average test order
and for moving-average test order  , perform the following steps.
, perform the following steps.
Let
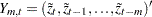 . Compute the following
. Compute the following 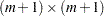 matrix
matrix 
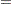
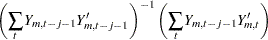
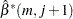
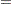


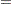
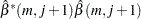
where
 ranges from
ranges from 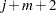 to
to  .
. Find the smallest eigenvalue,
 , of
, of  and its corresponding normalized eigenvector,
and its corresponding normalized eigenvector, 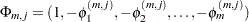 . The squared canonical correlation estimate is
. The squared canonical correlation estimate is  .
. Using the
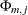 as AR(
as AR( ) coefficients, obtain the residuals for
) coefficients, obtain the residuals for 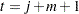 to
to  , by following the formula:
, by following the formula:  .
. From the sample autocorrelations of the residuals,
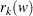 , approximate the standard error of the squared canonical correlation estimate by
, approximate the standard error of the squared canonical correlation estimate by 
where
 .
.
The test statistic to be used as an identification criterion is
 |
which is asymptotically 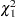 if
if 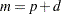 and
and  or if
or if 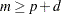 and
and 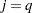 . For
. For 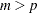 and
and 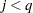 , there is more than one theoretical zero canonical correlation between
, there is more than one theoretical zero canonical correlation between 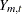 and
and  . Since the
. Since the 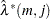 are the smallest canonical correlations for each
are the smallest canonical correlations for each  , the percentiles of
, the percentiles of 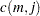 are less than those of a
are less than those of a 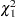 ; therefore, Tsay and Tiao (1985) state that it is safe to assume a
; therefore, Tsay and Tiao (1985) state that it is safe to assume a 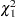 . For
. For 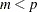 and
and  , no conclusions about the distribution of
, no conclusions about the distribution of 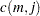 are made.
are made.
A SCAN table is then constructed using 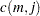 to determine which of the
to determine which of the 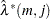 are significantly different from zero (see Table 7.7). The ARMA orders are tentatively identified by finding a (maximal) rectangular pattern in which the
are significantly different from zero (see Table 7.7). The ARMA orders are tentatively identified by finding a (maximal) rectangular pattern in which the 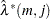 are insignificant for all test orders
are insignificant for all test orders 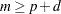 and
and 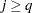 . There may be more than one pair of values (
. There may be more than one pair of values ( ) that permit such a rectangular pattern. In this case, parsimony and the number of insignificant items in the rectangular pattern should help determine the model order. Table 7.8 depicts the theoretical pattern associated with an ARMA(2,2) series.
) that permit such a rectangular pattern. In this case, parsimony and the number of insignificant items in the rectangular pattern should help determine the model order. Table 7.8 depicts the theoretical pattern associated with an ARMA(2,2) series.
MA |
||||||
AR |
0 |
1 |
2 |
3 |
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MA |
||||||||
AR |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
* |
X |
X |
X |
X |
X |
X |
X |
1 |
* |
X |
X |
X |
X |
X |
X |
X |
2 |
* |
X |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
* |
X |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
* |
X |
0 |
0 |
0 |
0 |
0 |
0 |
X = significant terms |
||||||||
0 = insignificant terms |
||||||||
* = no pattern |
||||||||
Copyright © SAS Institute, Inc. All Rights Reserved.