| The MDC Procedure |
| HEV and Multinomial Probit: Heteroscedastic Utility Function |
When the stochastic components of utility are heteroscedastic and independent, you can model the data by using an HEV or a multinomial probit model. The HEV model assumes that the utility of alternative 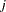 for each individual
for each individual  has heteroscedastic random components,
has heteroscedastic random components,
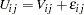 |
where the cumulative distribution function of the Gumbel distributed 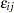 is
is
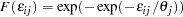 |
Note that the variance of 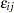 is
is 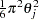 . Therefore, the error variance is proportional to the square of the scale parameter
. Therefore, the error variance is proportional to the square of the scale parameter 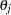 . For model identification, at least one of the scale parameters must be normalized to 1. The following SAS statements estimate an HEV model under a unit scale restriction for mode "1" (
. For model identification, at least one of the scale parameters must be normalized to 1. The following SAS statements estimate an HEV model under a unit scale restriction for mode "1" (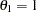 ). The results of computation are presented in Output 17.14 and Output 17.15.
). The results of computation are presented in Output 17.14 and Output 17.15.
/*-- hev with gauss-laguerre method --*/
proc mdc data=newdata;
model decision = ttime /
type=hev
nchoice=3
hev=(unitscale=1, integrate=laguerre)
covest=hess;
id pid;
run;
| Model Fit Summary | |
|---|---|
| Dependent Variable | decision |
| Number of Observations | 50 |
| Number of Cases | 150 |
| Log Likelihood | -33.41383 |
| Maximum Absolute Gradient | 0.0000218 |
| Number of Iterations | 11 |
| Optimization Method | Dual Quasi-Newton |
| AIC | 72.82765 |
| Schwarz Criterion | 78.56372 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
| ttime | 1 | -0.4407 | 0.1798 | -2.45 | 0.0143 |
| SCALE2 | 1 | 0.7765 | 0.4348 | 1.79 | 0.0741 |
| SCALE3 | 1 | 0.5753 | 0.2752 | 2.09 | 0.0366 |
The parameters SCALE2 and SCALE3 in the output correspond to the estimates of the scale parameters 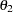 and
and 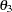 , respectively.
, respectively.
Note that the estimate of the HEV model is not always stable since computation of the log-likelihood function requires numerical integration. Bhat (1995) proposed the Gauss-Laguerre method. In general, the log-likelihood function value of HEV should be larger than that of conditional logit since HEV models include the conditional logit as a special case, but in this example the reverse is true (–33.414 for the HEV model, which is less than –33.321 for the conditional logit model). (See Figure 17.14 and Figure 17.3.) This indicates that the Gauss-Laguerre approximation to the true probability is too coarse. You can see how well the Gauss-Laguerre method works by specifying a unit scale restriction for all modes, as in the following statements, since the HEV model with the unit variance for all modes reduces to the conditional logit model:
/*-- hev with gauss-laguerre and unit scale --*/
proc mdc data=newdata;
model decision = ttime /
type=hev
nchoice=3
hev=(unitscale=1 2 3, integrate=laguerre)
covest=hess;
id pid;
run;
Figure 17.16 shows that the ttime coefficient is not close to that of the conditional logit model.
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
| ttime | 1 | -0.2926 | 0.0438 | -6.68 | <.0001 |
There is another option of specifying the integration method. The INTEGRATE=HARDY option uses the adaptive Romberg-type integration method. The adaptive integration produces much more accurate probability and log-likelihood function values, but often it is not practical to use this method of analyzing the HEV model since it requires excessive CPU time. The following SAS statements produce the HEV estimates by using the adaptive Romberg-type integration method. The results are displayed in Figure 17.17 and Figure 17.18.
/*-- hev with adaptive integration --*/
proc mdc data=newdata;
model decision = ttime /
type=hev
nchoice=3
hev=(unitscale=1, integrate=hardy)
covest=hess;
id pid;
run;
| Model Fit Summary | |
|---|---|
| Dependent Variable | decision |
| Number of Observations | 50 |
| Number of Cases | 150 |
| Log Likelihood | -33.02598 |
| Maximum Absolute Gradient | 0.0001202 |
| Number of Iterations | 8 |
| Optimization Method | Dual Quasi-Newton |
| AIC | 72.05197 |
| Schwarz Criterion | 77.78803 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
| ttime | 1 | -0.4580 | 0.1861 | -2.46 | 0.0139 |
| SCALE2 | 1 | 0.7757 | 0.4283 | 1.81 | 0.0701 |
| SCALE3 | 1 | 0.6908 | 0.3384 | 2.04 | 0.0412 |
With the INTEGRATE=HARDY option, the log-likelihood function value of the HEV model, 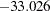 , is greater than that of the conditional logit model,
, is greater than that of the conditional logit model, 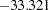 . (See Figure 17.17 and Figure 17.3.)
. (See Figure 17.17 and Figure 17.3.)
When you impose unit scale restrictions on all choices, as in the following statements, the HEV model gives the same estimates as the conditional logit model. (See Figure 17.19 and Figure 17.6.)
/*-- hev with adaptive integration and unit scale --*/
proc mdc data=newdata;
model decision = ttime /
type=hev
nchoice=3
hev=(unitscale=1 2 3, integrate=hardy)
covest=hess;
id pid;
run;
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
| ttime | 1 | -0.3572 | 0.0776 | -4.60 | <.0001 |
For comparison, we estimate a heteroscedastic multinomial probit model by imposing a zero restriction on the correlation parameter, 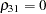 . The MDC procedure requires normalization of at least two of the error variances in the multinomial probit model. Also, for identification, the correlation parameters associated with a unit normalized variance are restricted to be zero. When the UNITVARIANCE= option is specified, the zero restriction on correlation coefficients applies to the last choice of the list. In the following statements, the variances of the first and second choices are normalized. The UNITVARIANCE=(1 2) option imposes additional restrictions that
. The MDC procedure requires normalization of at least two of the error variances in the multinomial probit model. Also, for identification, the correlation parameters associated with a unit normalized variance are restricted to be zero. When the UNITVARIANCE= option is specified, the zero restriction on correlation coefficients applies to the last choice of the list. In the following statements, the variances of the first and second choices are normalized. The UNITVARIANCE=(1 2) option imposes additional restrictions that 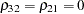 . The default for the UNITVARIANCE= option is the last two choices (which would have been equivalent to UNITVARIANCE=(2 3) for this example). The result is presented in Figure 17.20.
. The default for the UNITVARIANCE= option is the last two choices (which would have been equivalent to UNITVARIANCE=(2 3) for this example). The result is presented in Figure 17.20.
The utility function can be defined as
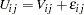 |
where
 |
/*-- mprobit estimation --*/
proc mdc data=newdata;
model decision = ttime /
type=mprobit
nchoice=3
unitvariance=(1 2)
covest=hess;
id pid;
restrict RHO_31 = 0;
run;
| Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
Parameter Label |
| ttime | 1 | -0.3206 | 0.0920 | -3.49 | 0.0005 | |
| STD_3 | 1 | 1.6913 | 0.6906 | 2.45 | 0.0143 | |
| RHO_31 | 0 | 0 | 0 | |||
| Restrict1 | 1 | 1.1854 | 1.5490 | 0.77 | 0.4499* | Linear EC [ 1 ] |
Note that in the output the estimates of standard errors and correlations are denoted by STD_i and RHO_ij, respectively. In this particular case the first two variances (STD_1, STD_2) are normalized to one, and corresponding correlations (RHO_21, RHO_32) are set to zero, so they are not listed among parameter estimates.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.