| The MDC Procedure |
| Parameter Heterogeneity: Mixed Logit |
One way of modeling unobserved heterogeneity across individuals in their sensitivity to observed exogenous variables is to use the mixed logit model with a random parameters or random coefficients specification. The probability of choosing alternative 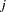 is written as
is written as
 |
where 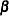 is a vector of coefficients that varies across individuals, and
is a vector of coefficients that varies across individuals, and 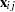 is a vector of exogenous attributes.
is a vector of exogenous attributes.
For example, you can specify the distribution of the parameter 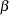 to be the normal distribution.
to be the normal distribution.
The mixed logit model uses a Monte Carlo simulation method to estimate the probabilities of choice. There are two simulation methods available. When the RANDNUM=PSEUDO option is given in the MODEL statement, pseudo-random numbers are generated, while the RANDNUM=HALTON option uses Halton quasi-random sequences. The default value is RANDNUM=HALTON.
You can estimate the model with normally distributed random coefficients of ttime with the following SAS statements:
/*-- mixed logit estimation --*/
proc mdc data=newdata type=mixedlogit;
model decision = ttime /
nchoice=3
mixed=(normalparm=ttime);
id pid;
run;
Let 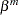 and
and 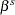 be mean and scale parameters, respectively, for the random coefficient,
be mean and scale parameters, respectively, for the random coefficient, 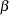 . The relevant utility function is
. The relevant utility function is
 |
where 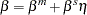 ;
; 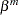 and
and 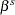 are fixed mean and scale parameters, respectively. The stochastic component,
are fixed mean and scale parameters, respectively. The stochastic component, 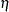 , is assumed to be standard normal since the NORMALPARM= option is given. Alternatively, the UNIFORMPARM= or LOGNORMALPARM= option can be specified. The LOGNORMALPARM= option is useful when nonnegative parameters are being estimated. The NORMALPARM=, UNIFORMPARM=, and LOGNORMALPARM= variables must be included on the right-hand side of the MODEL statement. See the section Mixed Logit Model for more details. To estimate a mixed logit model by using the transportation mode choice data, the MDC procedure requires the MIXED= option for random components. Results of the mixed logit estimation are displayed in Figure 17.21.
, is assumed to be standard normal since the NORMALPARM= option is given. Alternatively, the UNIFORMPARM= or LOGNORMALPARM= option can be specified. The LOGNORMALPARM= option is useful when nonnegative parameters are being estimated. The NORMALPARM=, UNIFORMPARM=, and LOGNORMALPARM= variables must be included on the right-hand side of the MODEL statement. See the section Mixed Logit Model for more details. To estimate a mixed logit model by using the transportation mode choice data, the MDC procedure requires the MIXED= option for random components. Results of the mixed logit estimation are displayed in Figure 17.21.
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
| ttime_M | 1 | -0.5342 | 0.2184 | -2.45 | 0.0144 |
| ttime_S | 1 | 0.2843 | 0.1911 | 1.49 | 0.1368 |
Note that the parameter ttime_M corresponds to the constant mean parameter  and the parameter ttime_S corresponds to the constant scale parameter
and the parameter ttime_S corresponds to the constant scale parameter  of the random coefficient
of the random coefficient 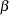 .
.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.