The HPCOUNTREG Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Missing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionParameter Naming Conventions for the RESTRICT, TEST, BOUNDS, and INIT StatementsComputational ResourcesCovariance Matrix TypesDisplayed OutputOUTPUT OUT= Data SetOUTEST= Data SetODS Table Names
Missing ValuesPoisson RegressionConway-Maxwell-Poisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Conway-Maxwell-Poisson RegressionZero-Inflated Negative Binomial RegressionParameter Naming Conventions for the RESTRICT, TEST, BOUNDS, and INIT StatementsComputational ResourcesCovariance Matrix TypesDisplayed OutputOUTPUT OUT= Data SetOUTEST= Data SetODS Table Names -
Examples

- References
Zero-Inflated Conway-Maxwell-Poisson Regression
Subsections:
In the Conway-Maxwell-Poisson regression model, the data generation process is defined as
![\[ P(Y_{i}=y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) = \frac{1}{Z(\lambda _{i},\nu _{i})} \frac{\lambda _{i}^{y_{i}}}{(y_{i}!)^{\nu _{i}}}, \quad y_ i = 0,1,2,\ldots \]](images/etshpug_hpcountreg0063.png)
where the normalization factor is
![\[ Z(\lambda _ i,\nu _ i) = \sum _{n=0}^{\infty }\frac{\lambda _{i}^{n}}{(n!)^{\nu _{i}}} \]](images/etshpug_hpcountreg0064.png)
and
![\[ \lambda _{i} = \exp (\mathbf{x}_{i}^{\prime } \bbeta ) \]](images/etshpug_hpcountreg0065.png)
![\[ \nu _{i}=-\exp (\mathbf{g}_{i}^{\prime } \delta ) \]](images/etshpug_hpcountreg0066.png)
The zero-inflated Conway-Maxwell-Poisson model can be written as
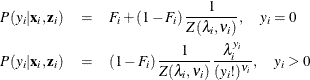
The conditional expectation and conditional variance of 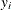 are given respectively by
are given respectively by
![\[ E(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) = (1 -F_{i})\frac{1}{Z(\lambda ,\nu )} \sum _{j=0}^{\infty }\frac{j \lambda ^{j}}{(j!)^{\nu }} \]](images/etshpug_hpcountreg0170.png)
![\[ V(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) = (1 -F_{i})\frac{1}{Z(\lambda ,\nu )} \sum _{j=0}^{\infty }\frac{j^{2} \lambda ^{j}}{(j!)^{\nu }}-E(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i})^2 \]](images/etshpug_hpcountreg0171.png)
The general form of the log-likelihood function for the Conway-Maxwell-Poisson zero-inflated model is
![\[ \mathcal{L} = \sum _{i=1}^{N}w_ i\ln \left[ P(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) \right] \]](images/etshpug_hpcountreg0172.png)
Zero-Inflated Conway-Maxwell-Poisson Model with Logistic Link Function
For this model, the probability 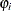 is expressed by using a logistic link function as
is expressed by using a logistic link function as
![\[ \varphi _{i}=\Lambda (\mathbf{z}_{i}’\bgamma )=\frac{\exp (\mathbf{z}_{i}'\bgamma )}{1+\exp (\mathbf{z}_{i}'\bgamma )} \]](images/etshpug_hpcountreg0173.png)
The log-likelihood function is
![\begin{eqnarray*} \mathcal{L} & = & \sum _{\{ i: y_{i}=0\} }w_ i\ln \left\{ \Lambda (\mathbf{z}_{i}’\bgamma ) + \left[ 1- \Lambda (\mathbf{z}_{i}’\bgamma )\right] \frac{1}{Z(\lambda _{i},\nu _{i})} \right\} \\ & + & \sum _{\{ i: y_{i}>0\} }w_ i\left\{ \ln \left[ \left( 1-\Lambda (\mathbf{z}_{i}’\bgamma )\right) \right] - ln(Z(\lambda ,\nu )) + (y_{i}\ln (\lambda ) - \nu \ln (y_ i!) \right\} \end{eqnarray*}](images/etshpug_hpcountreg0174.png)
Zero-Inflated Conway-Maxwell-Poisson Model with Normal Link Function
For this model, the probability 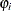 is specified by using the standard normal distribution function (probit function):
is specified by using the standard normal distribution function (probit function): 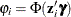 .
.
The log-likelihood function is written as
![\begin{eqnarray*} \mathcal{L} & = & \sum _{\{ i: y_{i}=0\} }w_ i\ln \left\{ \Phi (\mathbf{z}_{i}’\bgamma ) + \left[ 1- \Phi (\mathbf{z}_{i}’\bgamma )\right] \frac{1}{Z(\lambda _{i},\nu _{i})} \right\} \\ & + & \sum _{\{ i: y_{i}>0\} }w_ i\left\{ \ln \left[ \left( 1-\Phi (\mathbf{z}_{i}’\bgamma )\right) \right] - ln(Z(\lambda ,\nu )) + (y_{i}\ln (\lambda ) - \nu \ln (y_ i!) \right\} \end{eqnarray*}](images/etshpug_hpcountreg0175.png)