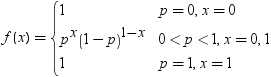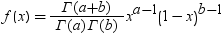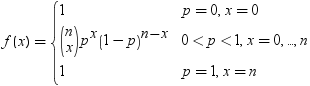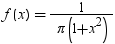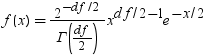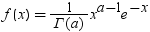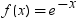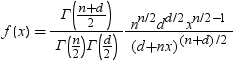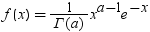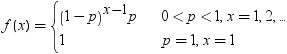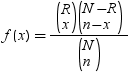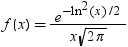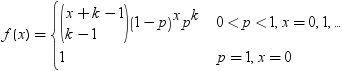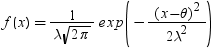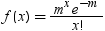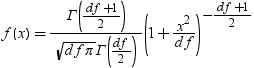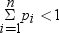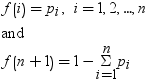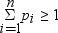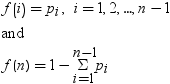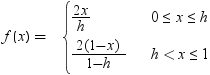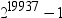RAND関数

分布	引数
Bernoulli	`BERNOULLI`
ベータ	`BETA`
二項	`BINOMIAL`
コーシー	`CAUCHY`
カイ2乗	`CHISQUARE`
Erlang	`ERLANG`
指数	`EXPONENTIAL`
F	`F`
ガンマ	`GAMMA`
幾何	`GEOMETRIC`
超幾何	`HYPERGEOMETRIC`
対数正規	`LOGNORMAL`
負の二項	`NEGBINOMIAL`
正規	`NORMAL\|GAUSSIAN`
Poisson	`POISSON`
T	`T`
テーブル	`TABLE`
三角	`TRIANGLE`
一様	`UNIFORM`
Weibull	`WEIBULL`

注: TおよびF以外は、最初の4文字によってどのような分布でも最小限に識別できます。

parameter-1, …, parameter-k

特定の分布に適した形状、位置または尺度パラメータの値を指定する数値定数、変数または式です(省略可能)。

参照項目

詳細

乱数の生成

乱数ストリームの再現

Mersenne-Twister RNGアルゴリズムの重複する値

乱数の生成

RAND関数は、さまざまな連続分布および離散分布から乱数を生成します。可能な場合、最も単純な形式の分布が使用されます。

RAND関数は、松本と西村(1998)によって開発されたMersenne-Twister乱数ジェネレータ(RNG)を応用しています。乱数ジェネレータには、長い周期(2¹⁹⁹³⁷-1)と高品質な統計的特性を有しています。この周期はMersenne素数で、RNGの名前はこれに由来します。アルゴリズムは、名前の後半部分を説明する、ひねり(twist)を入れた一般化フィードバックシフトレジスタ(TGFSR)です。TGFSRを使用したRNGでは、高次元(32ビット精度の623次元)の均等分布が生成されます。これは、623次元疑似乱数の連続ベクトル間の相関性が非常に小さいことを意味します。

RAND関数は単一のシードで開始します。ただし、プロセスの状態を単一のシードで捕捉することはできません。ジェネレータを停止し、停止時点から再開することはできません。

乱数ストリームの再現

乱数の再現可能なストリームを作成するには、CALL STREAMINITルーチンを使用して乱数生成のシード値を指定します。RAND関数が起動される前に、DATAステップごとにCALL STREAMINITルーチンを1回使用します。CALL STREAMINITルーチンの呼び出しを省略すると(またはCALL STREAMINITルーチンで正以外のシード値を指定すると)、RANDはシステムクロックへの呼び出しを使用してシードを取得します。詳細については、CALL STREAMINIT乱数の再現可能なストリームの作成を参照してください。

Mersenne-Twister RNGアルゴリズムの重複する値

Permutations RNGアルゴリズムには長い周期が使用されますが、大きなランダムサンプルに重複する値がないことを暗に示すものではありません。RAND関数は最大で2³²個の重複しない値を返します。サイズが10⁵のランダム一様サンプルでは、少なくとも1つの重複を引き当てる確率が50%を超えます。サイズMのランダム一様サンプルの期待重複数は、Mが2³²よりかなり小さいとき、約M²/2³³になります。たとえば、サイズM=10⁶のランダム一様サンプルでは、約115個の重複が期待されます。これらの結果は、確率論における有名な“誕生日の一致問題”で説明できます。

Bernoulli分布

x=RAND('BERNOULLI', p)

引数

x

次の確率密度関数を使用した分布のオブザベーションです。

table with 1 row and 1 column , row1 column 1 , f , open x close , equals left brace . table with 3 rows and 2 columns , row1 column 1 , 1 , column 2 p equals 0 comma x equals 0 , row2 column 1 , p to the x . open 1 minus p close super 1 minus x end super , column 2 0 less than p less than 1 comma x equals 0 comma 1 , row3 column 1 , 1 , column 2 p equals 1 comma x equals 1 , end table , end table. 別の形式を利用するにはイメージをクリックします。

範囲

x = 0, 1

p

成功確率を指定する数値定数、変数または式です。

範囲

0 ≤ p ≤ 1

ベータ分布

x=RAND('BETA', a, b)

引数

x

次の確率密度関数を使用した分布のオブザベーションです。

$table with 1 row and 1 column , row1 column 1 , f , open x close , equals . fraction cap gamma . open eh plus b close , over cap gamma , open eh close , cap gamma , open b close end fraction . x super eh minus 1 end super . open 1 minus x close super b minus 1 end super , end table. 別の形式を利用するにはイメージをクリックします。$

範囲

0 < x < 1

a

形状パラメータを指定する数値定数、変数または式です。

範囲

a > 0

b

形状パラメータを指定する数値定数、変数または式です。

範囲

b > 0

二項分布

x=RAND('BINOMIAL', p, n)

引数

x

次の確率密度関数を使用した分布からの整数オブザベーションです。

範囲	x = 0, 1, ..., n

p

成功確率を指定する数値定数、変数または式です。

範囲

0 ≤ p ≤ 1

n

独立Bernoulli試行数を数える整数のパラメータです。

範囲	n = 1, 2, ...

Cauchy分布

x=RAND('CAUCHY')

引数

x

次の確率密度関数を使用した分布のオブザベーションです。

$table with 1 row and 1 column , row1 column 1 , f , open x close , equals . fraction 1 , over pi . open 1 plus , x squared , close end fraction , end table. 別の形式を利用するにはイメージをクリックします。$

範囲	–∞ < x < ∞

カイ2乗分布

x=RAND('CHISQUARE', df)

引数

x

次の確率密度関数を使用した分布のオブザベーションです。

$table with 1 row and 1 column , row1 column 1 , f , open x close , equals . fraction 2 super negative d f slash 2 end super , over cap gamma . open , fraction d f , over 2 end fraction , close end fraction . x . super d f slash 2 minus 1 end super . e super negative x slash 2 end super , end table. 別の形式を利用するにはイメージをクリックします。$

範囲

x > 0

df

自由度を指定する数値定数、変数または式です。

範囲

df > 0

Erlang分布

x=RAND('ERLANG', a)

引数

x

次の確率密度関数を使用した分布のオブザベーションです。

$table with 1 row and 1 column , row1 column 1 , f , open x close , equals . fraction 1 , over cap gamma , open eh close end fraction . x super eh minus 1 end super . e super negative x end super , end table. 別の形式を利用するにはイメージをクリックします。$

範囲

x > 0

a

形状パラメータを指定する数値定数、変数または式です。

範囲	a = 1, 2, ...

指数分布

x=RAND('EXPONENTIAL')

引数

x

次の確率密度関数を使用した分布のオブザベーションです。

table with 1 row and 1 column , row1 column 1 , f , open x close , equals , e super negative x end super , end table. 別の形式を利用するにはイメージをクリックします。

範囲

x > 0

F分布

x=RAND('F', n, d)

引数

x

次の確率密度関数を使用した分布のオブザベーションです。

$table with 1 row and 1 column , row1 column 1 , f , open x close , equals . fraction cap gamma . open . fraction n plus d , over 2 end fraction . close , over cap gamma . open , n over 2 , close . cap gamma . open , d over 2 , close end fraction . fraction n super n slash 2 end super . d super d slash 2 end super . x super n slash 2 minus 1 end super , over open d plus n x close super open n plus d close . slash 2 end super end fraction , end table. 別の形式を利用するにはイメージをクリックします。$

範囲

x > 0

n

分子の自由度を指定する数値定数、変数または式です。

範囲

n > 0

d

分母の自由度を指定する数値定数、変数または式です。

範囲

d > 0

ガンマ分布

x=RAND('GAMMA', a)

引数

x

次の確率密度関数を使用した分布のオブザベーションです。

範囲

x > 0

a

形状パラメータを指定する数値定数、変数または式です。

範囲

a > 0

幾何分布

x=RAND('GEOMETRIC', p)

引数

x

1回の成功を得るために必要な試行回数を示す整数の度数です。Xは次の確率密度関数を使用した分布からの整数オブザベーションです。

table with 1 row and 1 column , row1 column 1 , f , open x close , equals left brace . table with 2 rows and 2 columns , row1 column 1 , open 1 minus p close super x minus 1 end super . p , column 2 0 less than p less than 1 comma x equals 1 comma 2 comma . . . , row2 column 1 , 1 , column 2 p equals 1 comma x equals 1 , end table , end table. 別の形式を利用するにはイメージをクリックします。

範囲	x = 1, 2, …

p

成功確率を指定する数値定数、変数または式です。

範囲

0 < p ≤ 1

超幾何分布

x=RAND('HYPER', N, R, n)

引数

x

次の確率密度関数を使用した分布からの整数オブザベーションです。

$table with 1 row and 1 column , row1 column 1 , f , open x close , equals . fraction , matrix with 2 rows and 1 column , row1 column 1 , r , row2 column 1 , x , end matrix . matrix with 2 rows and 1 column , row1 column 1 , n minus r , row2 column 1 , n minus x , end matrix , over , matrix with 2 rows and 1 column , row1 column 1 , n , row2 column 1 , n , end matrix end fraction , end table. 別の形式を利用するにはイメージをクリックします。$

範囲	x = max(0, (n – (N – R))), ..., min(n, R)

N

整数の母集団サイズを指定する数値定数、変数または式です。

範囲	N = 1, 2, ...

R

対象カテゴリの整数の項目数を指定する数値定数、変数または式です。

範囲	R = 0, 1, ..., N

n

整数のサンプルサイズパラメータを指定する数値定数、変数または式です。

範囲	n = 1, 2, ..., N

超幾何分布は、N個のボールが壺に入っており、そのうちのR個が赤のときに、壺からn個のボールを取り出す実験を数学的に形式化したものです。超幾何分布は、n個のサンプル中の赤いボールの数の分布です。

対数正規分布

x=RAND('LOGNORMAL')

引数

x

次の確率密度関数を使用した分布のオブザベーションです。

$table with 1 row and 1 column , row1 column 1 , f , open x close , equals . fraction e super negative , natural log of squared . open x close , slash 2 end super , over x , square root of 2 pi end root end fraction , end table. 別の形式を利用するにはイメージをクリックします。$

範囲

x > 0

負数二項分布

x=RAND('NEGBINOMIAL', p, k)

引数

x

次の確率密度関数を使用した分布からの整数オブザベーションです。

table with 1 row and 1 column , row1 column 1 , f , open x close , equals left brace . table with 2 rows and 2 columns , row1 column 1 , . matrix with 2 rows and 1 column , row1 column 1 , x plus k minus 1 , row2 column 1 , k minus 1 , end matrix . open 1 minus p close to the x . p to the k , column 2 0 less than p less than 1 comma x equals 0 comma 1 comma . . . , row2 column 1 , 1 , column 2 p equals 1 comma x equals 0 , end table , end table. 別の形式を利用するにはイメージをクリックします。

範囲	x = 0, 1, ...

k

成功回数を示す整数パラメータです。ただし、整数ではないk値も使用できます。

範囲	k = 1, 2, ...

p

成功確率を指定する数値定数、変数または式です。

範囲

0 < p ≤ 1

負の二項分布は、同じ成功確率pで行う逐次独立試行でk回成功するまでの失敗回数の分布です。

正規分布

x=RAND('NORMAL',<θ, λ>)

引数

x

次の確率密度関数を使用した平均θおよび標準偏差λの正規分布のオブザベーションです。

$table with 1 row and 1 column , row1 column 1 , f , open x close , equals . fraction 1 , over lamda , square root of 2 pi end root end fraction . e x p . open negative . fraction open x minus theta close squared , over 2 , lamda squared end fraction . close , end table. 別の形式を利用するにはイメージをクリックします。$

範囲	–∞ < x < ∞

θ

平均パラメータを指定する数値定数、変数または式です。

デフォルト

λ

標準偏差パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	λ > 0

Poisson分布

x=RAND('POISSON', m)

引数

x

次の確率密度関数を使用した分布からの整数オブザベーションです。

$table with 1 row and 1 column , row1 column 1 , f , open x close , equals . fraction m to the x . e super negative m end super , over x factorial end fraction , end table. 別の形式を利用するにはイメージをクリックします。$

範囲	x = 0, 1, ...

m

平均パラメータを指定する数値定数、変数または式です。

範囲

m > 0

T分布

x=RAND('T', df)

引数

x

次の確率密度関数を使用した分布のオブザベーションです。

$table with 1 row and 1 column , row1 column 1 , f , open x close , equals . fraction cap gamma . open . fraction d f plus 1 , over 2 end fraction . close , over square root of d f pi end root , cap gamma . open , fraction d f , over 2 end fraction , close end fraction . open 1 plus . fraction x squared , over d f end fraction . close super negative . fraction d f plus 1 , over 2 end fraction end super , end table. 別の形式を利用するにはイメージをクリックします。$

範囲	–∞ < x < ∞

df

自由度を指定する数値定数、変数または式です。

範囲

df > 0

テーブル分布

x=RAND('TABLE', p1, p2, ...)

引数

x

次のいずれかの分布からの整数のオブザベーションです。

次の場合、

modified cap sigma with i equals 1 below and with n above . p sub i , less than 1. 別の形式を利用するにはイメージをクリックします。

xはこの確率分布関数のオブザベーションです。

table with 3 rows and 1 column , row1 column 1 , f , open i close , equals , p sub i , comma i equals 1 comma 2 comma dot dot dot comma n , row2 column 1 , eh n d , row3 column 1 , f . open n plus 1 close . equals 1 minus . modified cap sigma with i equals 1 below and with n above . p sub i , end table. 別の形式を利用するにはイメージをクリックします。

次の場合、

modified cap sigma with i equals 1 below and with n above . p sub i , greater than or equal to 1. 別の形式を利用するにはイメージをクリックします。

がインデックスnで成り立つならば、xはこの確率分布関数のオブザベーションです。

table with 3 rows and 1 column , row1 column 1 , f , open i close , equals , p sub i , comma i equals 1 comma 2 comma dot dot dot comma n minus 1 , row2 column 1 , eh n d , row3 column 1 , f , open n close , equals 1 minus . modified cap sigma with i equals 1 below and with n minus 1 above . p sub i , end table. 別の形式を利用するにはイメージをクリックします。

p1, p2, ...

数値の確率値です。

範囲	0 ≤ p1, p2, ...≤ 1
制限事項	確率パラメータの最大数は動作環境によって異なりますが、パラメータの最大数は少なくとも32,767です。

テーブル分布は、指定した確率で値1、2、...、nを取ります。

注: FORMATステートメントを使用することにより、セット{1, 2, ..., n}をn個以下の要素セットにマップできます。

三角分布

x=RAND('TRIANGLE', h)

引数

x

次の確率密度関数を使用した分布のオブザベーションです。

$table with 1 row and 2 columns , row1 column 1 , f , open x close , equals , column 2 left brace . table with 2 rows and 2 columns , row1 column 1 , fraction 2 x , over h end fraction , column 2 0 less than or equal to x less than or equal to h , row2 column 1 , fraction 2 . open 1 minus x close , over 1 minus h end fraction , column 2 h less than x less than or equal to 1 , end table , end table. 別の形式を利用するにはイメージをクリックします。$

この式では、0≤h≤1になります。

範囲	0 ≤ x ≤ 1
注	分布は簡単に移動および調整できます。

h

三角の頂点の水平位置を指定する数値定数、変数または式です。

範囲

0≤h≤1

一様分布

x=RAND('UNIFORM')

引数

x

次の確率密度関数を使用した分布のオブザベーションです。

table with 1 row and 1 column , row1 column 1 , f , open x close , equals 1 , end table. 別の形式を利用するにはイメージをクリックします。

範囲

0 < x < 1

RAND関数が使用する一様乱数ジェネレータは、Mersenne-Twister(松本と西村(1998))です。このジェネレータには次の周期と

2 super 1 9 9 3 7 end super . minus 1. 別の形式を利用するにはイメージをクリックします。

最大で32ビットの精度で623次元の均等分布があります。このアルゴリズムは、RAND関数で使用できるほかの分布のジェネレータの基礎となります。

Weibull分布

x=RAND('WEIBULL', a, b)

引数

x

次の確率密度関数を使用した分布のオブザベーションです。

$table with 1 row and 1 column , row1 column 1 , f , open x close , equals , fraction eh , over b to the eh end fraction . x super eh minus 1 end super . e super negative . open , x over b , close to the eh end super , end table. 別の形式を利用するにはイメージをクリックします。$

範囲

x ≥ 0

a

形状パラメータを指定する数値定数、変数または式です。

範囲

a > 0

b

尺度パラメータを指定する数値定数、変数または式です。

範囲

b > 0

例

SASステートメントとその結果を次に示します。

SASステートメント	結果
x=rand('BERN', .75);	0
x=rand('BETA', 3, 0.1);	.99920
x=rand('BINOM', 0.75, 10);	10
x=rand('CAUCHY');	-1.41525
x=rand('CHISQ', 22);	25.8526
x=rand('ERLANG', 7);	7.67039
x=rand('EXPO');	1.48847
x=rand('F', 12, 322);	1.99647
x=rand('GAMMA', 7.25);	6.59588
x=rand('GEOM', 0.02);	43
x=rand('HYPER', 10, 3, 5);	1
x=rand('LOGN');	0.66522
x=rand('NEGB', 0.8, 5);	33
x=rand('NORMAL');	1.03507
x=rand('POISSON', 6.1);	6
x=rand('T', 4);	2.44646
x=rand('TABLE', .2, .5);	2
x=rand('TRIANGLE', 0.7);	.63811
x=rand('UNIFORM');	.96234
x=rand('WEIB', 0.25, 2.1);	6.55778

参考文献

Fishman, G. S. 1996. Monte Carlo:Concepts, Algorithms, and Applications. New York, 米国: Springer-Verlag.

Fushimi, M., and S. Tezuka. “The k-Distribution of Generalized Feedback Shift Register Pseudorandom Numbers.” 1983. Communications of the ACM 26: 516-255.

Gentle, J. E. 1998. Random Number Generation and Monte Carlo Methods. New York, 米国: Springer-Verlag.

Lewis, T. G., and W. H. Payne. “Generalized Feedback Shift Register Pseudorandom Number Algorithm.” 1973. Journal of the ACM 20: 456-468.

Matsumoto, M., and Y. Kurita. “Twisted GFSR Generators.” 1992. ACM Transactions on Modeling and Computer Simulation 2: 179-255.

Matsumoto, M., and Y. Kurita. “Twisted GFSR Generators II.” 1994. ACM Transactions on Modeling and Computer Simulation 4: 254-255.

Matsumoto, M., and T. Nishimura. “Mersenne Twister:A 623–Dimensionally Equidistributed Uniform Pseudo-Random Number Generator.” 1998. ACM Transactions on Modeling and Computer Simulation 8: 3-255.

Ripley, B. D. 1987. Stochastic Simulation. New York, 米国: Wiley.

Robert, C. P., and G. Casella. 1999. Monte Carlo Statistical Methods. New York, 米国: Springer-Verlag.

Ross, S. M. 1997. Simulation. San Diego, 米国: Academic Press.

RAND関数

構文

必須引数

distribution

parameter-1, …, parameter-k

詳細

乱数の生成

乱数ストリームの再現

Mersenne-Twister RNGアルゴリズムの重複する値

Bernoulli分布

x

p

ベータ分布

x

a

b

二項分布

x

p

n

Cauchy分布

x

カイ2乗分布

x

df

Erlang分布

x

a

指数分布

x

F分布

x

n

d

ガンマ分布

x

a

幾何分布

x

p

超幾何分布

x

N

R

n

対数正規分布

x

負数二項分布

x

k

p

正規分布

x

θ

λ

Poisson分布

x

m

T分布

x

df

テーブル分布

x

p1, p2, ...

三角分布

x

h

一様分布

x

Weibull分布

x

a

b

例

関連項目:

参考文献