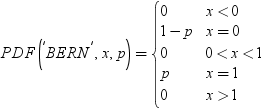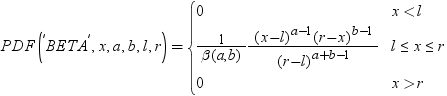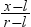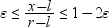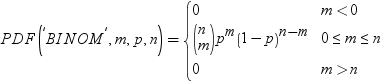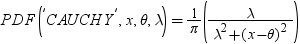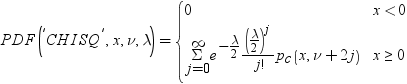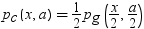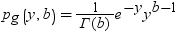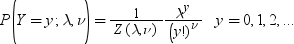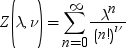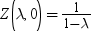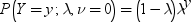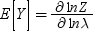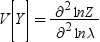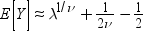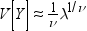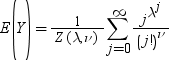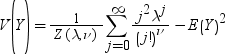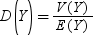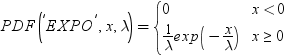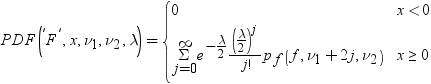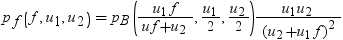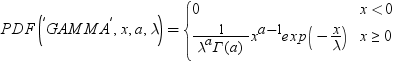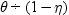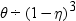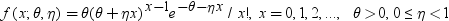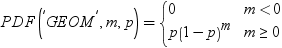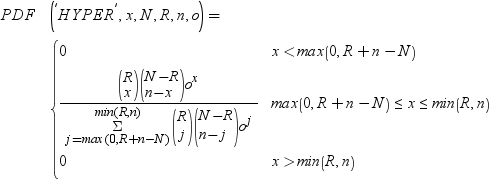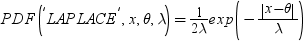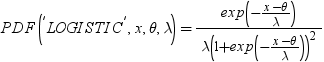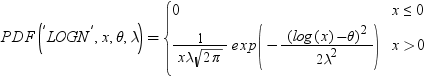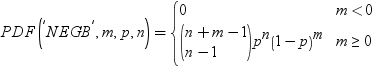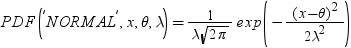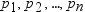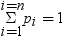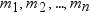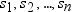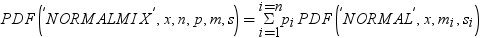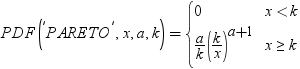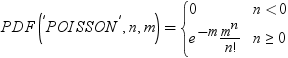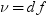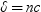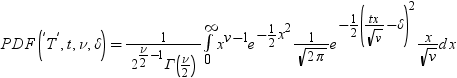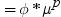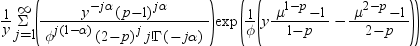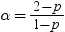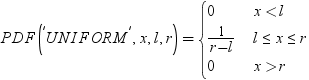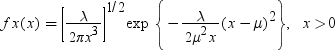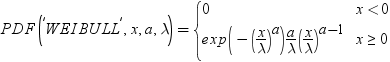PDF関数

分布	引数
Bernoulli	`Bernoulli`
ベータ	`BETA`
二項	`BINOMIAL`
コーシー	`CAUCHY`
カイ2乗	`CHISQUARE`
Conway-Maxwell-Poisson	`CMP`
指数	`EXPONENTIAL`
F	`F`
ガンマ	`GAMMA`
一般化Poisson	`GENPOISSON`
幾何	`GEOMETRIC`
超幾何	`HYPERGEOMETRIC`
Laplace	`LAPLACE`
ロジスティック	`LOGISTIC`
対数正規	`LOGNORMAL`
負の二項	`NEGBINOMIAL`
正規	`NORMAL\|GAUSS`
正規混合	`NORMALMIX`
パレート	`PARETO`
Poisson	`POISSON`
T	`T`
Tweedie	`TWEEDIE`
一様	`UNIFORM`
逆ガウス(Wald)	`WALD\|IGAUSS`
Weibull	`WEIBULL`

注	T、FおよびNORMALMIXを除き、最初の4文字で分布を最小限に識別できます。

quantile

確率変数の値を指定する数値定数、変数または式です。

オプション引数

parameter-1, ..., parameter-k

特定の分布に適した形状、位置または尺度パラメータの値を指定する数値定数、変数または式です(省略可能)。

参照項目	詳細これらのパラメータの詳細については、を参照してください。

詳細

Conway-Maxwell-Poisson分布

Bernoulli分布

PDF ('BERNOULLI', x, p)

引数

x

確率変数を指定する数値定数、変数または式です。

p

成功確率を指定する数値定数、変数または式です。

範囲

0 ≤ p ≤ 1

詳細

Bernoulli分布のPDF関数は、Bernoulli分布(成功確率はp)の確率密度関数を返します。PDF関数は、値xで評価されます。式は次のとおりです。

table with 1 row and 1 column , row1 column 1 , p d f . open prime b e r n prime comma x comma p close . equals left brace . table with 5 rows and 2 columns , row1 column 1 , 0 , column 2 x less than 0 , row2 column 1 , 1 minus p , column 2 x equals 0 , row3 column 1 , 0 , column 2 0 less than x less than 1 , row4 column 1 , p , column 2 x equals 1 , row5 column 1 , 0 , column 2 x greater than 1 , end table , end table. 別の形式を利用するにはイメージをクリックします。

注: この分布には、位置または尺度パラメータはありません。

ベータ分布

PDF ('BETA', x, a, b <, l, r>)

引数

x

確率変数を指定する数値定数、変数または式です。

a

形状パラメータを指定する数値定数、変数または式です。

範囲

a > 0

b

形状パラメータを指定する数値定数、変数または式です。

範囲

b > 0

l

左位置パラメータを指定する数値定数、変数または式です。

デフォルト

r

右位置パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	r > l

詳細

ベータ分布のPDF関数は、ベータ分布(形状パラメータはaおよびb)の確率密度関数を返します。PDF関数は、値xで評価されます。式は次のとおりです。

$table with 1 row and 1 column , row1 column 1 , p d f . open prime b e t , eh prime , comma x comma eh comma b comma l comma r close . equals left brace . table with 3 rows and 2 columns , row1 column 1 , 0 , column 2 x less than l , row2 column 1 , fraction 1 , over beta . open eh comma b close end fraction . fraction open x minus l close super eh minus 1 end super . open r minus x close super b minus 1 end super , over open r minus l close super eh plus b minus 1 end super end fraction , column 2 l less than or equal to x less than or equal to r , row3 column 1 , 0 , column 2 x greater than r , end table , end table. 別の形式を利用するにはイメージをクリックします。$

注: 数量 $fraction x minus l , over r minus l end fraction. 別の形式を利用するにはイメージをクリックします。$ は、強制的に $epsilon less than or equal to . fraction x minus l , over r minus l end fraction . less than or equal to 1 minus 2 epsilon. 別の形式を利用するにはイメージをクリックします。$ .

二項分布

PDF ('BINOMIAL', m, p, n)

引数

m

成功数を数える整数の確率変数です。

範囲	m = 0, 1, ...

p

成功確率を指定する数値定数、変数または式です。

範囲

0 ≤ p ≤ 1

n

独立Bernoulli試行数を数える整数のパラメータです。

範囲	n = 0, 1, ...

詳細

二項分布のPDF関数は、値mで評価される二項分布(パラメータはpおよびn)の確率密度関数を返します。式は次のとおりです。

table with 1 row and 1 column , row1 column 1 , p d f . open prime b i n o , m prime , comma m comma p comma n close . equals left brace . table with 3 rows and 2 columns , row1 column 1 , 0 , column 2 m less than 0 , row2 column 1 , , matrix with 2 rows and 1 column , row1 column 1 , n , row2 column 1 , m , end matrix . p to the m . open 1 minus p close super n minus m end super , column 2 0 less than or equal to m less than or equal to n , row3 column 1 , 0 , column 2 m greater than n , end table , end table. 別の形式を利用するにはイメージをクリックします。

注: 二項分布には、位置または尺度パラメータはありません。

Cauchy分布

PDF ('CAUCHY', x <, θ, λ>)

引数

x

確率変数を指定する数値定数、変数または式です。

θ

位置パラメータを指定する数値定数、変数または式です。

デフォルト

λ

尺度パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	λ > 0

詳細

Cauchy分布のPDF関数は、Cauchy分布(位置パラメータはθ、尺度パラメータはλ)の確率密度関数を返します。PDF関数は、値xで評価されます。式は次のとおりです。

$table with 1 row and 1 column , row1 column 1 , p d f . open prime c eh u c h y prime comma x comma theta comma lamda close . equals , fraction 1 , over pi end fraction . open . fraction lamda , over lamda squared , plus . open x minus theta close squared end fraction . close , end table. 別の形式を利用するにはイメージをクリックします。$

カイ2乗分布

PDF ('CHISQUARE', x, df <, nc>)

引数

x

確率変数を指定する数値定数、変数または式です。

df

自由度を指定する数値定数、変数または式です。

範囲

df > 0

nc

省略可能な非心度パラメータを指定する数値定数、変数または式です。

範囲

nc ≥ 0

詳細

カイ2乗分布のPDF関数は、カイ2乗分布(自由度はdf、非心度パラメータはnc)の確率密度関数を返します。PDF関数は、値xで評価されます。この関数では、整数以外の自由度を使用できます。ncが省略されているかゼロの場合、心度カイ2乗分布の値が返されます。次の式は、カイ2乗分布のPDF関数を表しています。

$table with 1 row and 1 column , row1 column 1 , p d f . open prime c h i s q prime comma x comma nu comma lamda close . equals left brace . table with 2 rows and 2 columns , row1 column 1 , 0 , column 2 x less than 0 , row2 column 1 , modified cap sigma with j equals 0 below and with infinity above . e super negative , lamda over 2 end super . fraction open , lamda over 2 , close to the j , over j factorial end fraction . p sub c . open x comma nu plus 2 j close , column 2 x greater than or equal to 0 , end table , end table. 別の形式を利用するにはイメージをクリックします。$

この式では、p_c(.,.)は、心度カイ2乗分布の密度を示しています。

table with 1 row and 1 column , row1 column 1 , p sub c . open x comma eh close . equals , 1 half , p sub g . open , x over 2 , comma , eh over 2 , close , end table. 別の形式を利用するにはイメージをクリックします。

この式では、p_g(y,b)は、次の式によって得られるガンマ分布の密度です。

$table with 1 row and 1 column , row1 column 1 , p sub g . open y comma b close . equals . fraction 1 , over cap gamma , open b close end fraction . e super negative y end super . y super b minus 1 end super , end table. 別の形式を利用するにはイメージをクリックします。$

Conway-Maxwell-Poisson分布

PDF('CONMAXPOI',y,λ,ν)

引数

y

カウントを表す負でない整数を指定する数値定数、変数または式です。

λ

Poisson平均パラメータに似た位置パラメータを指定する数値定数、変数または式です。

ν

ばらつきのパラメータを指定する数値定数、変数または式です。

詳細

Conway-Maxwell-Poisson (CMP)分布はPoisson分布の一般化です。これにより、過小分散データと過大分散データをモデル化できます。CMP分布は、次の式に従って定義されます。

$p open y equals y semicolon lambda comma nu close equals . fraction 1 , over z open lambda comma nu close end fraction . fraction lambda to the y , over open y , factorial close to the nu end fraction. 別の形式を利用するにはイメージをクリックします。$

正規化因子は次の式で表されます。

$z open lambda comma nu close equals . sum , from , n equals 0 , to , infinity , of . fraction lambda to the n , over open n factorial close to the nu end fraction. 別の形式を利用するにはイメージをクリックします。$

λおよびνは負ではなく、同時にゼロにもなりません。

追加パラメータνの導入では、分布の裾挙動のモデル化における柔軟性が考慮されています。ν=1の場合、比はPoisson分布の減衰率に等しくなります。ν<1の場合、減衰率が減少し、Poisson分布より裾が長いプロセス(過大分散データ)をモデル化できます。ν>1の場合、減衰率が非線形方法で増加し、したがって、分布の裾が短くなります(過小分散データ)。

Conway-Maxwell-Poisson分布には、いくつか特殊なケースがあります。λ<1およびν→∞の場合、結果的にConway-Maxwell-Poisson分布がBernoulli分布になります。このケースでは、データが取り得る値は0および1です。これは極過小分散を表します。ν=1の場合、等分散の特性を持つPoisson分布に戻ります。ν=0およびλ<1の場合、正規化因子は収束性であり、次の幾何級数を形成します。

$z open lambda comma 0 close equals . fraction 1 , over 1 minus lambda end fraction. 別の形式を利用するにはイメージをクリックします。$

確率密度関数は、次の式で表されます。

p open y equals y semicolon lambda comma nu equals 0 close equals open 1 minus lambda close , lambda to the y. 別の形式を利用するにはイメージをクリックします。

幾何分布は、著しい過大分散のケースを表します。

Conway-Maxwell-Poissonモデルの平均、分散およびばらつき

Conway-Maxwell-Poisson分布の平均および分散は、次の式で定義されます。

$e left bracket y right bracket equals . fraction partial 1 n z , over partial 1 n lambda end fraction. 別の形式を利用するにはイメージをクリックします。$

$v left bracket y right bracket equals . fraction partial squared , 1 n z , over partial squared , 1 n lambda end fraction. 別の形式を利用するにはイメージをクリックします。$

Conway-Maxwell-Poisson分布は、そのパラメータλおよびνに関して、その積率の閉形式を持ちません。ただし、積率は近似できます。(Conway-Maxwell-Poisson分布および離散データの詳細については、この関数の最後にあるリファレンスセクションを参照してください。)次の式で示すように、Zに対する漸近表現を使用すると、E(Y)およびV(Y)を導き出せます。

$e left bracket y right bracket almost equal to . lambda super 1 slash nu end super . plus , fraction 1 , over 2 nu end fraction , minus , 1 half. 別の形式を利用するにはイメージをクリックします。$

v left bracket y right bracket almost equal to , 1 over nu . lambda super 1 slash nu end super. 別の形式を利用するにはイメージをクリックします。

Conway-Maxwell-Poissonモデルでは、対数展開を使用して無限級数の総和が評価されます。(Conway-Maxwell-Poisson分布および離散データの詳細については、この関数の最後にあるリファレンスセクションを参照してください。)Conway-Maxwell-Poissonモデルについては、次のように平均および分散が計算されます。

$e open y close equals . fraction 1 , over z open lambda comma nu close end fraction . sum , from , j equals 0 , to , infinity , of . fraction j super lambda to the j end super , over open j factorial close to the nu end fraction. 別の形式を利用するにはイメージをクリックします。$

$v open y close equals . fraction 1 , over z open lambda comma nu close end fraction . sum , from , j equals 0 , to , infinity , of . fraction j squared , lambda to the j , over open j factorial close to the nu end fraction . minus e . open y close squared. 別の形式を利用するにはイメージをクリックします。$

ばらつきは、次のように定義されます。

$d open y close equals . fraction v open y close , over e open y close end fraction. 別の形式を利用するにはイメージをクリックします。$

指数分布

PDF ('EXPONENTIAL', x <, λ>)

引数

x

確率変数を指定する数値定数、変数または式です。

λ

尺度パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	λ > 0

詳細

指数分布のPDF関数は、指数分布(尺度パラメータはλ)の確率密度関数を返します。PDF関数は、値xで評価されます。式は次のとおりです。

table with 1 row and 1 column , row1 column 1 , p d f . open prime e x p o prime comma x comma lamda close . equals left brace . table with 2 rows and 2 columns , row1 column 1 , 0 , column 2 x less than 0 , row2 column 1 , 1 over lamda , e x p . open negative , x over lamda , close , column 2 x greater than or equal to 0 , end table , end table. 別の形式を利用するにはイメージをクリックします。

F分布

PDF ('F', x, ndf, ddf <, nc>)

引数

x

確率変数を指定する数値定数、変数または式です。

ndf

分子の自由度を指定する数値定数、変数または式です。

範囲

ndf> 0

ddf

分母の自由度を指定する数値定数、変数または式です。

範囲

ddf > 0

nc

省略可能な非心度パラメータを指定する数値定数、変数または式です。

範囲

nc ≥ 0

詳細

F分布のPDF関数は、F分布(分子の自由度はndf、分母の自由度はddf、非心度パラメータはnc)の確率密度関数を返します。PDF関数は、値xで評価されます。このPDF関数では、ndfおよびddfに対して整数以外の自由度を使用できます。ncが除外されているかゼロの場合、心度F分布の値が返されます。次の式では、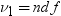

nu sub 1 , equals n d f. 別の形式を利用するにはイメージをクリックします。

、

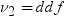nu sub 2 , equals d d f. 別の形式を利用するにはイメージをクリックします。

、

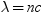lamda equals n c. 別の形式を利用するにはイメージをクリックします。

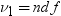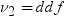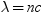とします。次の式は、F分布のPDF関数を表しています。

$table with 1 row and 1 column , row1 column 1 , p d f . open prime , f prime , comma x comma , nu sub 1 , comma , nu sub 2 , comma lamda close . equals left brace . table with 2 rows and 2 columns , row1 column 1 , 0 , column 2 x less than 0 , row2 column 1 , modified cap sigma with j equals 0 below and with infinity above . e super negative , lamda over 2 end super . fraction open , lamda over 2 , close to the j , over j factorial end fraction . p sub f . open f comma , nu sub 1 , plus 2 j comma , nu sub 2 , close , column 2 x greater than or equal to 0 , end table , end table. 別の形式を利用するにはイメージをクリックします。$

この式では、p_f(f,u₁,u₂)は、次の式を使用した心度F分布の密度です。

$table with 1 row and 1 column , row1 column 1 , p sub f . open f comma , u sub 1 , comma , u sub 2 , close . equals , p sub b . open . fraction u sub 1 , f , over u f plus , u sub 2 end fraction . comma , fraction u sub 1 , over 2 end fraction , comma , fraction u sub 2 , over 2 end fraction , close . fraction u sub 1 , u sub 2 , over open , u sub 2 , plus , u sub 1 , f close squared end fraction , end table. 別の形式を利用するにはイメージをクリックします。$

この式では、p_B(x,a,b)は、標準ベータ分布の密度です。

注: F分布には、位置または尺度パラメータはありません。

ガンマ分布

PDF ('GAMMA', x, a <, λ>)

引数

x

確率変数を指定する数値定数、変数または式です。

a

形状パラメータを指定する数値定数、変数または式です。

範囲

a > 0

λ

尺度パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	λ > 0

詳細

ガンマ分布のPDF関数は、ガンマ分布(形状パラメータはa、尺度パラメータはλ)の確率密度関数を返します。PDF関数は、値xで評価されます。式は次のとおりです。

$table with 1 row and 1 column , row1 column 1 , p d f . open prime g eh m m eh prime comma x comma eh comma lamda close . equals left brace . table with 2 rows and 2 columns , row1 column 1 , 0 , column 2 x less than 0 , row2 column 1 , fraction 1 , over lamda to the eh , cap gamma , open eh close end fraction . x super eh minus 1 end super . e x p . open negative , x over lamda , close , column 2 x greater than or equal to 0 , end table , end table. 別の形式を利用するにはイメージをクリックします。$

一般化Poisson分布

PDF ('GENPOISSON', x, θ, η)

引数

x

整数の確率変数を指定する数値定数、変数または式です。

θ

形状パラメータを指定する数値定数、変数または式です。

範囲	<10⁵ and >0

η

形状パラメータを指定する数値定数、変数または式です。

範囲	≥0かつ<0.95
ヒント	η =0の場合、平均と分散がθのPoisson分布になります。η>0の場合、平均はで、分散はです。

詳細

一般化Poisson分布の確率質量関数の次のとおりです。

f open x semicolon theta comma eta close equals theta . open theta plus eta x close super x minus 1 end super . e super negative theta minus eta x end super . slash x factorial comma x equals 0 comma 1 comma 2 comma ... comma theta greater than 0 comma 0 less than or equal to eta less than 1. 別の形式を利用するにはイメージをクリックします。

幾何分布

PDF ('GEOMETRIC', m, p)

引数

m

初めて成功する前の失敗数を指定する数値定数、変数または式です。

範囲

m ≥ 0

p

成功確率を指定する数値定数、変数または式です。

範囲

0 ≤ p ≤ 1

詳細

幾何分布のPDF関数は、幾何分布(パラメータはp)の確率密度関数を返します。PDF関数は、値mで評価されます。式は次のとおりです。

table with 1 row and 1 column , row1 column 1 , p d f . open prime g e o m prime comma m comma p close . equals left brace . table with 2 rows and 2 columns , row1 column 1 , 0 , column 2 m less than 0 , row2 column 1 , p . open 1 minus p close to the m , column 2 m greater than or equal to 0 , end table , end table. 別の形式を利用するにはイメージをクリックします。

注: この分布には、位置または尺度パラメータはありません。

超幾何分布

PDF ('HYPER', x, N, R, n <, o>)

引数

x

整数の確率変数を指定する数値定数、変数または式です。

N

整数の母集団サイズを指定する数値定数、変数または式です。

範囲	N = 1, 2, ...

R

対象カテゴリの整数の項目数を指定する数値定数、変数または式です。

範囲	R = 0, 1, ..., N

n

整数のサンプルサイズパラメータを指定する数値定数、変数または式です。

範囲	n = 1, 2, ..., N

o

省略可能なオッズ比パラメータを指定する数値定数、変数または式です。

範囲

o > 0

詳細

超幾何分布のPDF関数は、拡張超幾何分布(母集団サイズはN、項目数はR、サンプルサイズはn、オッズ比はo)の確率密度関数を返します。PDF関数は、値xで評価されます。oが除外されているか1の場合、一般超幾何分布の値が返されます。式は次のとおりです。

$table with 2 rows and 2 columns , row1 column 1 , p d f , column 2 open prime h y p e r prime comma x comma n comma r comma n comma o close . equals , row2 column 1 , , column 2 left brace . table with 3 rows and 2 columns , row1 column 1 , 0 , column 2 x less than m eh x . open 0 comma r plus n minus n close , row2 column 1 , fraction , matrix with 2 rows and 1 column , row1 column 1 , r , row2 column 1 , x , end matrix . matrix with 2 rows and 1 column , row1 column 1 , n minus r , row2 column 1 , n minus x , end matrix . o to the x , over modified cap sigma with j equals m eh x . open 0 comma r plus n minus n close below and with m i n . open r comma n close above , matrix with 2 rows and 1 column , row1 column 1 , r , row2 column 1 , j , end matrix . matrix with 2 rows and 1 column , row1 column 1 , n minus r , row2 column 1 , n minus j , end matrix . o to the j end fraction , column 2 m eh x . open 0 comma r plus n minus n close . less than or equal to x less than or equal to m i n . open r comma n close , row3 column 1 , 0 , column 2 x greater than m i n . open r comma n close , end table , end table. 別の形式を利用するにはイメージをクリックします。$

Laplace分布

PDF ('LAPLACE', x <, θ, λ>)

引数

x

確率変数を指定する数値定数、変数または式です。

θ

位置パラメータを指定する数値定数、変数または式です。

デフォルト

λ

尺度パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	λ > 0

詳細

Laplace分布のPDF関数は、Laplace分布(位置パラメータはθ、尺度パラメータはλ)の確率密度関数を返します。PDF関数は、値xで評価されます。式は次のとおりです。

$table with 1 row and 1 column , row1 column 1 , p d f . open prime l eh p l eh c , e prime , comma x comma theta comma lamda close . equals , fraction 1 , over 2 lamda end fraction , e x p . open negative . fraction absolute value of x minus theta , end absolute value , , over lamda end fraction . close , end table. 別の形式を利用するにはイメージをクリックします。$

ロジスティック分布

PDF ('LOGISTIC', x <, θ, λ>)

引数

x

確率変数を指定する数値定数、変数または式です。

θ

位置パラメータを指定する数値定数、変数または式です。

デフォルト

λ

尺度パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	λ > 0

詳細

ロジスティック分布のPDF関数は、ロジスティック分布(位置パラメータはθ、尺度パラメータはλ)の確率密度関数を返します。PDF関数は、値xで評価されます。式は次のとおりです。

$table with 1 row and 1 column , row1 column 1 , p d f . open prime l o g i s t i c prime comma x comma theta comma lamda close . equals . fraction e x p . open negative . fraction x minus theta , over lamda end fraction . close , over lamda . open 1 plus e x p . open negative . fraction x minus theta , over lamda end fraction . close . close squared end fraction , end table. 別の形式を利用するにはイメージをクリックします。$

対数正規分布

PDF ('LOGNORMAL', x <, θ, λ>)

引数

x

確率変数を指定する数値定数、変数または式です。

θ

対数尺度パラメータを指定する数値定数、変数または式です。exp(θ)は尺度パラメータです。

デフォルト

λ

形状パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	λ > 0

詳細

対数正規分布のPDF関数は、対数正規分布(対数尺度パラメータはθ、形状パラメータはλ)の確率密度関数を返します。PDF関数は、値xで評価されます。式は次のとおりです。

$table with 1 row and 1 column , row1 column 1 , p d f . open prime l o g n prime comma x comma theta comma lamda close . equals left brace . table with 2 rows and 2 columns , row1 column 1 , 0 , column 2 x less than or equal to 0 , row2 column 1 , fraction 1 , over x lamda , square root of 2 pi end root end fraction . e x p . open negative . fraction open l o g , open x close , minus theta close squared , over 2 , lamda squared end fraction . close , column 2 x greater than 0 , end table , end table. 別の形式を利用するにはイメージをクリックします。$

負数二項分布

PDF ('NEGBINOMIAL', m, p, n)

引数

m

失敗数を数える正の整数の確率変数を指定する、数値定数、変数または式です。

範囲	m= 0, 1, ...

p

成功確率を指定する数値定数、変数または式です。

範囲

0 ≤ p ≤ 1

n

成功数を数える値を指定する数値定数、変数または式です。

範囲

n > 0

詳細

負の二項分布のPDF関数は、負の二項分布(成功確率はp、成功数はn)の確率密度関数を返します。PDF関数は、値mで評価されます。式は次のとおりです。

table with 1 row and 1 column , row1 column 1 , p d f . open prime n e g b prime comma m comma p comma n close . equals left brace . table with 2 rows and 2 columns , row1 column 1 , 0 , column 2 m less than 0 , row2 column 1 , . matrix with 2 rows and 1 column , row1 column 1 , n plus m minus 1 , row2 column 1 , n minus 1 , end matrix . p to the n . open 1 minus p close to the m , column 2 m greater than or equal to 0 , end table , end table. 別の形式を利用するにはイメージをクリックします。

注: 負の二項分布には、位置または尺度パラメータはありません。

正規分布

PDF ('NORMAL', x <, θ, λ>)

引数

x

確率変数を指定する数値定数、変数または式です。

θ

位置パラメータを指定する数値定数、変数または式です。

デフォルト

λ

尺度パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	λ > 0

詳細

正規分布のPDF関数は、正規分布(位置パラメータはθ、尺度パラメータはλ)の確率密度関数を返します。PDF関数は、値xで評価されます。式は次のとおりです。

$table with 1 row and 1 column , row1 column 1 , p d f . open prime n o r m eh l prime comma x comma theta comma lamda close . equals . fraction 1 , over lamda , square root of 2 pi end root end fraction . e x p . open negative . fraction open x minus theta close squared , over 2 , lamda squared end fraction . close , end table. 別の形式を利用するにはイメージをクリックします。$

正規混合分布

PDF ('NORMALMIX', x, n, p₁, p₂, ... p_n, m₁, m₂, ... m_n, s₁, s₂, ... s_n)

引数

x

確率変数を指定する数値定数、変数または式です。

n

整数の混合数を指定する数値定数、変数または式です。

範囲	n = 1, 2, ...

p_i

n個の比率を指定する数値定数、変数または式のリストです。ここで、です。

範囲	p = 0, 1, ...

m_i

n個の平均を指定する数値定数、変数または式のリストです。

s_i

n個の標準偏差を指定する数値定数、変数または式のリストです。

範囲

s > 0

詳細

正規混合分布のPDF関数は、正規混合分布のオブザベーションがx以下となる確率を返します。式は次のとおりです。

table with 1 row and 1 column , row1 column 1 , p d f . open prime n o r m eh l m i x prime comma x comma n comma p comma m comma s close . equals . modified cap sigma with i equals 1 below and with i equals n above . p sub i p d f . open prime n o r m eh l prime comma x comma , m sub i , comma , s sub i , close , end table. 別の形式を利用するにはイメージをクリックします。

正規混合分布の重み付けは、負でないことが必要です。重み付けの合計が1に等しくない場合は相対的な重み付けとして扱われ、合計が1となるように調整されます。

注: 正規混合分布には、位置または尺度パラメータはありません。

パレート分布

PDF ('PARETO', x, a <, k>)

引数

x

数値の確率変数を指定する数値定数、変数または式です。

a

形状パラメータを指定する数値定数、変数または式です。

範囲

a > 0

k

尺度パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	k > 0

詳細

パレート分布のPDF関数は、パレート分布(形状パラメータはa、尺度パラメータはk)の確率密度関数を返します。PDF関数は、値xで評価されます。式は次のとおりです。

table with 1 row and 1 column , row1 column 1 , p d f . open prime p eh r e t o prime comma x comma eh comma k close . equals left brace . table with 2 rows and 2 columns , row1 column 1 , 0 , column 2 x less than k , row2 column 1 , eh over k . open , k over x , close super eh plus 1 end super , column 2 x greater than or equal to k , end table , end table. 別の形式を利用するにはイメージをクリックします。

Poisson分布

PDF ('POISSON', n, m)

引数

n

整数の確率変数を指定する数値定数、変数または式です。

範囲	n= 0, 1, ...

m

平均パラメータを指定する数値定数、変数または式です。

範囲

m > 0

詳細

Poisson分布のPDF関数は、Poisson分布(平均はm)の確率密度関数を返します。PDF関数は、値nで評価されます。式は次のとおりです。

$table with 1 row and 1 column , row1 column 1 , p d f . open prime p o i s s o n prime comma n comma m close . equals left brace . table with 2 rows and 2 columns , row1 column 1 , 0 , column 2 n less than 0 , row2 column 1 , e super negative m end super . fraction m to the n , over n factorial end fraction , column 2 n greater than or equal to 0 , end table , end table. 別の形式を利用するにはイメージをクリックします。$

注: Poisson分布には、位置または尺度パラメータはありません。

T分布

PDF ('T', t, df <, nc>)

引数

t

確率変数を指定する数値定数、変数または式です。

df

自由度を指定する数値定数、変数または式です。

範囲

df > 0

nc

省略可能な非心度パラメータを指定する数値定数、変数または式です。

詳細

T分布のPDF関数は、T分布(自由度はdf、非心度パラメータはnc)の確率密度関数を返します。PDF関数は、値xで評価されます。このPDF関数では、整数以外の自由度を使用できます。ncが除外されているかゼロの場合、心度T分布の値が返されます。次の式では、

、

delta equals n c. 別の形式を利用するにはイメージをクリックします。

とします。

$table with 1 row and 1 column , row1 column 1 , p d f . open prime t prime comma t comma nu comma delta close . equals . fraction 1 , over 2 super nu over 2 , minus 1 end super . cap gamma . open , nu over 2 , close end fraction . integral , from , 0 , to , infinity , of . x super v minus 1 end super . e super negative , 1 half , x squared end super . fraction 1 , over square root of 2 pi end root end fraction . e super negative , 1 half . open , fraction t x , over square root of v end fraction , minus delta close squared end super . fraction x , over square root of v end fraction , d x , end table. 別の形式を利用するにはイメージをクリックします。$

注: T分布には、位置または尺度パラメータはありません。

Tweedie分布

PDF ('TWEEDIE', y, p <, µ, φ>)

引数

y

確率変数を指定する数値定数、変数または式です。

範囲	y ≥0
注	この引数は必須です。
注	y>1の場合、yは数値になります。p=1の場合、yは整数になります。

p

累乗パラメータを指定する数値定数、変数または式です。

範囲	p ≥1
注	この引数は必須です。

µ

平均パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	µ >0

φ

ばらつきのパラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	φ>0

詳細

ツウィーディ分布のPDF関数は、式variance

equals straight phi times , mu to the p. 別の形式を利用するにはイメージをクリックします。

式は次のとおりです。

$1 over y . modified cap sigma with j equals 1 below and with infinity above . open . fraction y super negative j alpha end super . open . p minus 1 close super j alpha end super , over straight phi super j open 1 minus alpha close end super . open 2 minus p close to the j . j factorial cap gamma open negative j alpha close end fraction . close exp of open , 1 over straight phi , open y . fraction mu super 1 minus p end super . minus 1 , over 1 minus p end fraction . minus . fraction mu super 2 minus p end super . minus 1 , over 2 minus p end fraction . close close. 別の形式を利用するにはイメージをクリックします。$

前述の式には次の関係が適用されます。

$alpha equals . fraction 2 minus p , over 1 minus p end fraction. 別の形式を利用するにはイメージをクリックします。$

注: 計算されたツウィーディの確率の精度は、パラメータ空間における位置に大きく依存します。通常、10桁の精度を利用できますが、pの近似値が2の場合や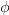

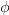の近似値が0の場合は、6桁の精度に低下する可能性があります。6桁の精度に低下する可能性があります。

注: 数値データでの問題を避けるため、µおよびΦは定数SQRTMACEPSより小さくしないようにします。

一様分布

PDF ('UNIFORM', x <, l, r>)

引数

x

確率変数を指定する数値定数、変数または式です。

l

左位置パラメータを指定する数値定数、変数または式です。

デフォルト

r

右位置パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	r > l

詳細

一様分布のPDF関数は、一様分布(左位置パラメータはl、右位置パラメータはr)の確率密度関数を返します。PDF関数は、値xで評価されます。式は次のとおりです。

$table with 1 row and 1 column , row1 column 1 , p d f . open prime u n i f o r m prime comma x comma l comma r close . equals left brace . table with 3 rows and 2 columns , row1 column 1 , 0 , column 2 x less than l , row2 column 1 , fraction 1 , over r minus l end fraction , column 2 l less than or equal to x less than or equal to r , row3 column 1 , 0 , column 2 x greater than r , end table , end table. 別の形式を利用するにはイメージをクリックします。$

逆ガウス(Wald)分布

PDF ('WALD', x, λ <, µ>)

PDF ('IGAUSS', x, λ <, µ>)

引数

x

確率変数を指定する数値定数、変数または式です。

λ

形状パラメータを指定する数値定数、変数または式です。

範囲

λ > 0

µ

平均パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	μ > 0

詳細

Wald分布のPDF関数は、値xで評価されるWald分布(形状パラメータはλ)の確率密度関数を返します。式は次のとおりです。

$f x open x close equals . left bracket . fraction lamda , over 2 pi x cubed end fraction . right bracket super 1 slash 2 end super . exp of left brace negative . fraction lamda , over 2 mu squared , x end fraction . open x minus mu close squared . right brace comma x greater than 0. 別の形式を利用するにはイメージをクリックします。$

Weibull分布

PDF('WEIBULL', x, a <, λ>)

引数

x

確率変数を指定する数値定数、変数または式です。

a

形状パラメータを指定する数値定数、変数または式です。

範囲

a > 0

λ

尺度パラメータを指定する数値定数、変数または式です。

デフォルト	1
範囲	λ > 0

詳細

Weibull分布のPDF関数は、Weibull分布(形状パラメータはa、尺度パラメータはλ)の確率密度関数を返します。PDF関数は、値xで評価されます。式は次のとおりです。

table with 1 row and 1 column , row1 column 1 , p d f . open prime w e i b u l l prime comma x comma eh comma lamda close . equals left brace . table with 2 rows and 2 columns , row1 column 1 , 0 , column 2 x less than 0 , row2 column 1 , e x p . open negative . open , x over lamda , close to the eh . close . eh over lamda . open , x over lamda , close super eh minus 1 end super , column 2 x greater than or equal to 0 , end table , end table. 別の形式を利用するにはイメージをクリックします。

例

SASステートメントとその結果を次に示します。

SASステートメント	結果
y=pdf('BERN', 0, .25);	0.75
y=pdf('BERN', 1, .25);	0.25
y=pdf('BETA', 0.2, 3, 4);	1.2288
y=pdf('BINOM', 4, .5, 10);	0.20508
y=pdf('CAUCHY', 2);	0.063662
y=pdf('CHISQ', 11.264, 11);	0.081686
y=pdf('CONMAXPOI', .2, 2.3, .4);	0.0097732635
y=pdf('EXPO', 1);	0.36788
y=pdf('F', 3.32, 2, 3);	0.054027
y=pdf('GAMMA', 1, 3);	0.18394
y=pdf('GENPOISSON', 9, 1, .7);	0.0150130915
y=pdf('GEOMETRIC', 5, .3);	y=0.050421
y=pdf('HYPER', 2, 200, 50, 10);	0.28685
y=pdf('LAPLACE', 1);	0.18394
y=pdf('LOGISTIC', 1);	0.19661
y=pdf('LOGNORMAL', 1);	0.39894
y=pdf('NEGB', 1, .5, 2);	0.25
y=pdf('NORMAL', 1.96);	0.058441
y=pdf('NORMALMIX',2.3, 3, .33, .33, .34, .5, 1.5, 2.5, .79, 1.6, 4.3);	0.1166
y=pdf('PARETO', 1, 1);	1
y=pdf('POISSON', 2, 1);	0.18394
y=pdf('T', .9, 5);	0.24194
y=pdf('TWEEDIE', .8, 5);	0.7422908236
y=pdf('UNIFORM', 0.25);	1
y=pdf('WALD', 1, 2);	0.56419
y=pdf('WEIBULL', 1, 2);	0.73576

参考文献

Shmueli, G., T. Minka,, S. Borle, and P. Boatwright. “A Useful Distribution for Fitting Discrete Data:Revival of the Conway-Maxwell-Poisson Distribution.” 2005. Applied Statistics : 54:127–142.