The IRT Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Notation for the Item Response Theory ModelAssumptionsPROC IRT Contrasted with Other SAS ProceduresResponse ModelsMarginal LikelihoodApproximating the Marginal LikelihoodMaximizing the Marginal LikelihoodFactor Score EstimationModel and Item FitItem and Test informationMissing ValuesOutput Data SetsODS Table NamesODS Graphics
Notation for the Item Response Theory ModelAssumptionsPROC IRT Contrasted with Other SAS ProceduresResponse ModelsMarginal LikelihoodApproximating the Marginal LikelihoodMaximizing the Marginal LikelihoodFactor Score EstimationModel and Item FitItem and Test informationMissing ValuesOutput Data SetsODS Table NamesODS Graphics -
Examples

- References
Item and Test information
Let 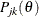 be the probability of endorsing category k for item j for a subject whose ability score is
be the probability of endorsing category k for item j for a subject whose ability score is 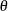 . Then the item information function can be defined as
. Then the item information function can be defined as
![\[ I_ j(\theta ) = \sum _{k=1}^{K} I_ k(\theta ) P_{jk}(\theta ) \]](images/statug_irt0129.png)
where
![\[ I_ k(\theta ) = -\frac{\partial ^2}{\partial \theta ^2}\log P_{jk}(\theta ) \]](images/statug_irt0130.png)
The test information function is the sum of the information functions of the items in the test. The information function of a test that has J items is
![\[ I(\theta ) = \sum _{j=1}^{J} I_ j(\theta ) \]](images/statug_irt0131.png)