The ICPHREG Procedure

Predicted Values

Given a new vector of covariates 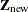$\bZ _{\mr{new}}$, the linear predictor is computed as 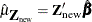$\hat{\mu }_{\bZ _{\mr{new}}}=\bZ _{\mr{new}}’\hat{\bbeta }$, where 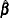$\hat{\bbeta }$ is the maximum likelihood estimate of 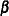$\bbeta $. The variance of 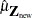$\hat{\mu }_{\bZ _{\mr{new}}}$ is estimated by

\[ \hat{\sigma }_{\bZ _{\mr{new}}}^2 = \bZ _{\mr{new}}’ \bSigma _{\hat{\bbeta }} \bZ _{\mr{new}} \]

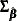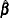where $\bSigma _{\hat{\bbeta }}$ denotes the estimated covariance matrix for $\hat{\bbeta }$.

Suppose the estimated baseline hazard is 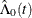$\hat{\Lambda }_0(t)$. Given 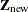$\bZ _{\mr{new}}$, the cumulative hazard function can be predicted by

\[ \hat{\Lambda }(t;\bZ _{\mr{new}}) = \hat{\Lambda }_0(t) e^{\bZ _{\mr{new}}'\hat{\bbeta }} \]

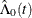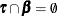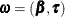Denote the vector of parameters that is used for obtaining $\hat{\Lambda }_0(t)$ as $\btau $. It is apparent that $\btau \cap \bbeta = \emptyset $. The vector of parameters that need to be estimated can be represented as $\bomega =(\bbeta ,\btau )$.

The variance of 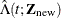$\hat{\Lambda }(t;\bZ _{\mr{new}})$ can be estimated by applying the delta method:

\[ \hat{\sigma }^2(\hat{\Lambda }(t;\bZ _{\mr{new}})) = P(t,\hat{\bomega })’ \bSigma P(t,\hat{\bomega }) \]

where

\[ P(t,\bomega ) = \frac{\partial \Lambda (t;\bZ _{\mr{new}})}{\partial \bomega } \]

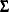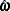and $\bSigma $ denotes the estimated covariance matrix for $\hat{\bomega }$.

Given 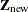$\bZ _{\mr{new}}$, the predicted survival function is estimated by

\[ \hat{S}(t;\bZ _{\mr{new}}) = \exp (\hat{\Lambda }(t;\bZ _{\mr{new}})) \]

The standard error of 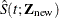$\hat{S}(t;\bZ _{\mr{new}})$ can be conveniently estimated by an application of the delta method:

\[ \hat{\sigma }(\hat{S}(t;\bZ _{\mr{new}})) = \hat{S}(t;\bZ _{\mr{new}}) \hat{\sigma }(\hat{\Lambda }(t;\bZ _{\mr{new}})) \]

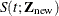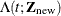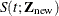By default, a natural log transformation is applied to obtain the pointwise confidence limits for $S(t;\bZ _{\mr{new}})$ and $\Lambda (t;\bZ _{\mr{new}})$. You can use the CLTYPE= option to specify a different transformation for $S(t;\bZ _{\mr{new}})$.