The VARIOGRAM Procedure
This example helps you explore aspects of automated semivariogram fitting with PROC VARIOGRAM. The test case is a spatial study of arsenic (As) concentration in drinking water.
Arsenic is a toxic pollutant that can occur in drinking water because of human activity or, typically, due to natural release
from the sediments in water aquifers. The World Health Organization has a standard that allows As concentration up to a maximum of 10 ![]() g/lt (micrograms per liter) in drinking water.
g/lt (micrograms per liter) in drinking water.
In general, natural release of arsenic into groundwater is very slow. Arsenic concentration in water might exhibit no significant
temporal fluctuations over a period of a few months. For this reason, it is acceptable to perform a spatial study of arsenic
with input from time-aggregated pollutant concentrations. This example makes use of this assumption for its data set logAsData. The data set consists of 138 simulated observations from wells across a square area of 500 km ![]() 500 km. The variable
500 km. The variable logAs in the logAsData data set is the natural logarithm of arsenic concentration. Often, the natural logarithm of arsenic concentration (logAs) is used as the random variable to facilitate the analysis because its distribution tends to resemble the normal distribution.
The goal is to explore spatial continuity in the logAs observations. The following statements read the logAs values from the logAsData data set:
title 'Semivariogram Model Fitting of Log-Arsenic Concentration'; data logAsData; input East North logAs @@; label logAs='log(As) Concentration'; datalines; 193.0 296.6 -0.68153 232.6 479.1 0.96279 268.7 312.5 -1.02908 43.6 4.9 0.65010 152.6 54.9 1.87076 449.1 395.8 0.95932 310.9 493.6 -1.66208 287.8 164.9 -0.01779 330.0 8.0 2.06837 225.7 241.7 0.15899 452.3 83.4 -1.21217 156.5 462.5 -0.89031 11.5 84.4 -0.24496 144.4 335.7 0.11950 149.0 431.8 -0.57251 234.3 123.2 -1.33642 37.8 197.8 -0.27624 183.1 173.9 -2.14558 149.3 426.7 -1.06506 434.4 67.5 -1.04657 439.6 237.0 -0.09074 36.4 175.2 -1.21211 370.6 244.0 3.28091 452.0 96.5 -0.77081 247.0 86.8 0.04720 413.6 373.2 1.78235 253.5 291.7 0.56132 129.7 111.9 1.34000 352.7 42.1 0.23621 279.3 82.7 2.12350 382.6 290.7 0.86756 188.2 222.8 -1.23308 382.8 154.5 -0.94094 304.4 309.2 -1.95158 337.5 387.2 -1.31294 490.7 189.8 0.40206 159.0 100.1 -0.22272 245.5 329.2 -0.26082 372.1 379.5 -1.89078 417.8 84.1 -1.25176 173.9 407.6 -0.24240 121.5 107.7 1.54509 453.5 313.6 0.65895 143.5 346.7 -0.87196 157.4 125.5 -1.96165 371.8 353.2 -0.59464 358.9 338.2 -1.07133 8.6 437.8 1.44203 395.9 394.2 -0.24144 149.5 58.9 1.17459 453.5 420.6 -0.63951 182.3 85.0 1.00005 21.0 290.1 0.31016 11.1 352.2 -0.88418 131.2 238.4 -0.57184 104.9 6.3 1.12054 247.3 256.0 0.14019 428.4 383.7 0.92448 327.8 481.1 -2.72543 199.2 92.8 -0.05717 453.9 230.1 0.16571 205.0 250.6 0.07581 459.5 271.6 0.93700 229.5 262.8 1.83590 370.4 228.6 2.96611 330.2 281.9 1.79723 354.8 388.3 -3.18262 406.2 222.7 2.41594 254.4 393.1 2.03221 96.7 85.2 -0.47156 407.2 256.8 0.66747 498.5 273.8 1.03041 417.2 471.4 -1.42766 368.8 424.3 -0.70506 303.0 59.1 1.43070 403.1 264.1 1.64554 21.2 360.8 0.67094 148.2 78.1 2.15323 305.5 310.7 -1.47985 228.5 180.3 -0.68386 161.1 143.3 1.07901 70.5 155.1 0.54652 363.1 282.6 -0.43051 86.0 472.5 -1.18855 175.9 105.3 -2.08112 96.8 426.3 1.56592 475.1 453.1 -1.53776 125.7 485.4 1.40054 277.9 201.6 -0.54565 406.2 125.0 -1.38657 60.0 275.5 -0.59966 431.3 494.6 -0.36860 399.9 399.0 -0.77265 28.8 311.1 0.91693 166.1 348.2 -0.49056 266.6 83.5 0.67277 54.7 356.3 0.49596 433.5 460.3 -1.61309 201.7 167.6 -1.40678 158.1 203.6 -1.32499 67.6 230.4 1.14672 81.9 250.0 0.63378 372.0 50.7 0.72445 26.4 264.6 1.00862 300.1 91.7 -0.74089 303.0 447.4 1.74589 108.4 386.2 1.12847 55.6 191.7 0.95175 36.3 273.2 1.78880 94.5 298.3 -2.43320 366.1 187.3 -0.80526 130.7 389.2 -0.31513 37.2 324.2 0.24489 295.5 211.8 0.41899 58.6 206.2 0.18495 346.3 142.8 -0.92038 484.2 215.9 0.08012 451.4 415.7 0.02773 58.9 86.5 0.17652 212.6 363.9 0.17215 378.7 407.6 0.51516 265.9 305.0 -0.30718 123.2 314.8 -0.90591 26.9 471.7 1.70285 16.5 7.1 0.51736 255.1 472.6 2.02381 111.5 148.4 -0.09658 440.4 375.0 1.23285 406.4 19.5 1.01181 321.2 65.8 -0.02095 466.4 357.1 -0.49272 2.0 484.6 0.50994 200.9 205.1 0.43543 30.3 337.0 1.60882 297.0 12.7 1.79824 158.2 450.7 0.05295 122.8 105.3 1.53936 417.8 329.7 -2.08124 ;
First you want to inspect the logAs data for surface trends and the pairwise distribution. You run the VARIOGRAM procedure with the NOVARIOGRAM option in the COMPUTE statement. You also request the PLOTS=PAIRS(MID) option, which prompts the pair distance plot to display the actual distance between pairs, rather than the lag number itself, in the midpoint of the lags. You use the following statements:
ods graphics on;
proc variogram data=logAsData plots=pairs(mid); compute novariogram nhc=50; coord xc=East yc=North; var logAs; run;
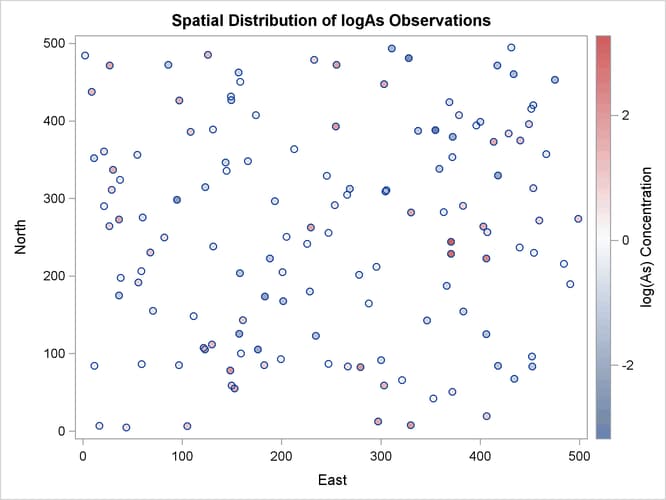
The observations scatter plot in Output 102.1.1 shows a rather uniform distribution of the locations in the study domain. Reasonably, neighboring values of logAs seem to exhibit some correlation. There seems to be no definite sign of an overall surface trend in the logAs values. You can consider that the observations are trend-free, and proceed with estimation of the empirical semivariance.
The observed logAs values go as high as 3.28091, which corresponds to a concentration of 26.6 ![]() g/lt. In fact, only three observations exceed the health standard of 10
g/lt. In fact, only three observations exceed the health standard of 10 ![]() g/lt (or about 2.3 in the log scale), and they are situated in relatively neighboring locations to the east of the domain
center.
g/lt (or about 2.3 in the log scale), and they are situated in relatively neighboring locations to the east of the domain
center.
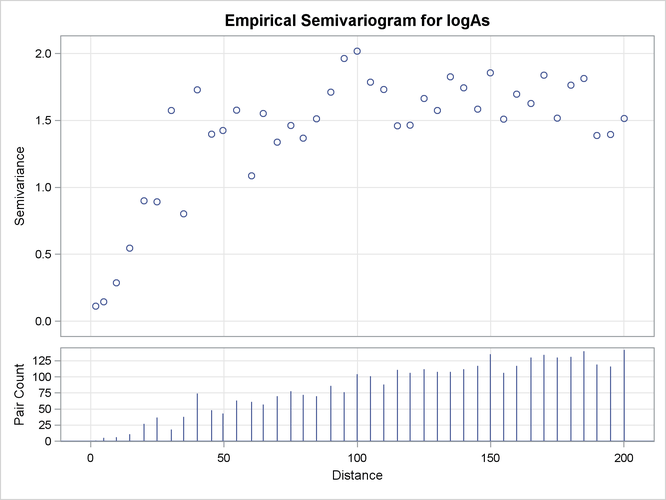
Based on the discussion in section Preliminary Spatial Data Analysis, the pair distance plot in Output 102.1.2 suggests that you could consider pairs that are anywhere around up to half the maximum pairwise distance of about 700 km.
After some experimentation with values for the LAGDISTANCE= and MAXLAGS= options, you actually find that a lag distance of 5 km over 40 lags can provide a clear representation of the logAs semivariance. With respect to Output 102.1.2, this finding indicates that in the current example it is sufficient to consider pairs separated by a distance of up to 200
km. You run the following statements to obtain the empirical semivariogram:
proc variogram data=logAsData plots(only)=semivar; compute lagd=5 maxlag=40; coord xc=East yc=North; var logAs; run;
The first few lag classes of the logAs empirical semivariance table are shown in Output 102.1.3.
Output 102.1.3: Partial Output of the Empirical Semivariogram Table for logAs Data
| Semivariogram Model Fitting of Log-Arsenic Concentration |
| The VARIOGRAM Procedure |
| Dependent Variable: logAs |
| Empirical Semivariogram |
| Lag Class |
Pair Count |
Average Distance |
Semivariance |
|---|---|---|---|
| 0 | 1 | 1.9 | 0.111 |
| 1 | 5 | 4.9 | 0.145 |
| 2 | 6 | 9.7 | 0.286 |
| 3 | 11 | 14.6 | 0.545 |
| 4 | 27 | 20.0 | 0.900 |
Output 102.1.3 and Output 102.1.4 indicate that the logarithm of arsenic spatial correlation starts with a small nugget effect around 0.11 and rises to a sill
value that is most likely between 1.4 and 1.8. The rise could be of exponential type, although the smooth increase of semivariance
close to the origin could also suggest Gaussian behavior. You suspect that a Matérn form might also work, since its smoothness
parameter ![]() can regulate the form to exhibit an intermediate behavior between the exponential and Gaussian forms.
can regulate the form to exhibit an intermediate behavior between the exponential and Gaussian forms.
You can investigate all of the preceding clues with the model fitting features of PROC VARIOGRAM. The simplest way to fit
a model is to specify its form in the MODEL statement. In this case, you have the added complexity of having more than one possible candidate. For this reason, you use
the FORM=AUTO option that picks the best fit out of a list of candidates. Within this option you specify the MLIST= suboption to use the exponential, Gaussian, and Matérn forms. You also specify the NEST= suboption to request fitting of a model with up to two nested structures. Eventually, you specify the PLOTS=FIT option to produce a plot of the fitted models. The STORE statement saves the fitting output into an item store you name SemivAsStore for future use. You apply these specifications with the following statements:
proc variogram data=logAsData plots(only)=fit; store out=SemivAsStore / label='LogAs Concentration Models'; compute lagd=5 maxlag=40; coord xc=East yc=North; model form=auto(mlist=(exp,gau,mat) nest=1 to 2); var logAs; run; ods graphics off;
The table of general information about fitting is shown in Output 102.1.5. The table lets you know that 12 model combinations are to be tested for weighted least squares fitting, based on the three forms that you specified.
Output 102.1.5: Semivariogram Model Fitting General Information
| Semivariogram Model Fitting of Log-Arsenic Concentration |
| Semivariogram Model Fitting | |
|---|---|
| Model | Selection from 12 form combinations |
| Output Item Store | WORK.SEMIVASSTORE |
| Item Store Label | LogAs Concentration Models |
The combinations include repetitions. For example, you specified the GAU form; hence the GAU-GAU form is tested, too. The
model combinations also include permutations. For example, you specified the GAU and the EXP forms; hence the GAU-EXP and
EXP-GAU models are fitted separately. According to the section Nested Models, it might seem that the same model is fitted twice. However, in each of these two cases, each structure starts the fitting
process with different parameter initial values. This can lead GAU-EXP to a different fit than EXP-GAU leads to, as seen in
the fitting summary table in Output 102.1.6. The table shows all the model combinations that were tested and fitted. By default, the ordering is based on the weighted
sum of squares error criterion, and you can see that the lowest values in the Weighted SSE column are in top slots of the list.
Output 102.1.6: Semivariogram Model Fitting Summary
| Fit Summary | |||
|---|---|---|---|
| Class | Model | Weighted SSE |
AIC |
| 1 | Gau-Gau | 25.42435 | -9.59246 |
| Gau-Mat | 25.42482 | -7.59169 | |
| 2 | Exp-Gau | 25.97835 | -8.70865 |
| 3 | Exp-Mat | 26.36846 | -6.09754 |
| 4 | Mat | 26.37519 | -10.08708 |
| 5 | Gau | 26.78629 | -11.45296 |
| 6 | Exp | 28.01200 | -9.61851 |
| Exp-Exp | 28.01200 | -5.61850 | |
| Mat-Exp | 28.01200 | -3.61850 | |
| Gau-Exp | 28.01200 | -5.61850 | |
Note the leftmost Class column in Output 102.1.6. As explained in detail in section Classes of Equivalence, when you fit more than one model, all fitted models that compute the same semivariance are placed in the same class of equivalence.
For example, in this fitting example the top ranked GAU-GAU and GAU-MAT nested models produce indistinguishable semivariograms;
for that reason they are both placed in the same class 1 of equivalence. The same occurs with the EXP, GAU-EXP, EXP-EXP, and
MAT-EXP models in the bottom of the table. By default, PROC VARIOGRAM uses the AIC as a secondary classification criterion;
hence models in each equivalence class are already ordered based on their AIC values.
Another remark in Output 102.1.6 is that despite submitting 12 model combinations for fitting, the table shows only 10. You can easily see that the combinations
MAT-GAU and MAT-MAT are not among the listed models in the fit summary. This results from the behavior of the VARIOGRAM procedure
in the following situation: A parameter optimization takes place during the fitting process. In the present case the optimizer
keeps increasing the Matérn smoothness parameter ![]() in the MAT-GAU model. At the limit of an infinite
in the MAT-GAU model. At the limit of an infinite ![]() parameter, the Matérn form becomes the Gaussian form. For that reason, when the parameter
parameter, the Matérn form becomes the Gaussian form. For that reason, when the parameter ![]() is driven towards very high values, PROC VARIOGRAM automatically replaces the Matérn form with the Gaussian. This switch
converts the MAT-GAU model into a GAU-GAU model. However, a GAU-GAU model already exists among the specified forms; consequently,
the duplicate GAU-GAU model is skipped, and the fitted model list is reduced by one model. A similar explanation justifies
the omission of the MAT-MAT model from the fit summary table.
is driven towards very high values, PROC VARIOGRAM automatically replaces the Matérn form with the Gaussian. This switch
converts the MAT-GAU model into a GAU-GAU model. However, a GAU-GAU model already exists among the specified forms; consequently,
the duplicate GAU-GAU model is skipped, and the fitted model list is reduced by one model. A similar explanation justifies
the omission of the MAT-MAT model from the fit summary table.
In our example, the nested Gaussian-Gaussian model is the fitting selection of the procedure based on the default ranking criteria. Output 102.1.7 displays additional information about the selected model. In particular, you see the table with general information about the Gaussian-Gaussian model, the initial values used for its parameters, and information about the optimization process for the fitting.
Output 102.1.7: Fitting and Optimization Information for Gaussian-Gaussian Model
| Semivariogram Model Fitting | |
|---|---|
| Name | Gaussian-Gaussian |
| Label | Gau-Gau |
| Model Information | |
|---|---|
| Parameter | Initial Value |
| Nugget | 0.0903 |
| GauScale1 | 0.6709 |
| GauRange1 | 100.0 |
| GauScale2 | 0.6709 |
| GauRange2 | 50.0230 |
| Optimization Information | |
|---|---|
| Optimization Technique | Dual Quasi-Newton |
| Parameters in Optimization | 5 |
| Lower Boundaries | 5 |
| Upper Boundaries | 0 |
| Starting Values From | PROC |
The estimated parameter values of the selected Gaussian-Gaussian model are shown in Output 102.1.8.
Output 102.1.8: Parameter Estimates of the Fitting Selected Model
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | Estimate | Approx Std Error |
DF | t Value | Approx Pr > |t| |
| Nugget | 0.08308 | 0.05097 | 36 | 1.63 | 0.1118 |
| GauScale1 | 0.3277 | 0.2077 | 36 | 1.58 | 0.1234 |
| GauRange1 | 62.3127 | 19.8488 | 36 | 3.14 | 0.0034 |
| GauScale2 | 1.2615 | 0.2070 | 36 | 6.10 | <.0001 |
| GauRange2 | 21.4596 | 3.2722 | 36 | 6.56 | <.0001 |
By default, when you specify more than one model to fit, PROC VARIOGRAM produces a fit plot that compares the first five classes of the successfully fit candidate models. The model that is selected according to the specified fitting criteria is shown with a thicker line in the plot.
You can modify the number of displayed equivalence classes with the NCLASSES= suboption of the PLOTS=FIT option. When you have such comparison plots, PROC VARIOGRAM displays the representative model from each class of equivalence.
The default fit plot for the current model comparison is shown in Output 102.1.9. The legend informs you there is one more model in the first class of equivalence, as the fitting summary table indicated earlier in Output 102.1.6.
Output 102.1.9: Fitted Theoretical and Empirical logAs Concentration Semivariograms for the Specified Models
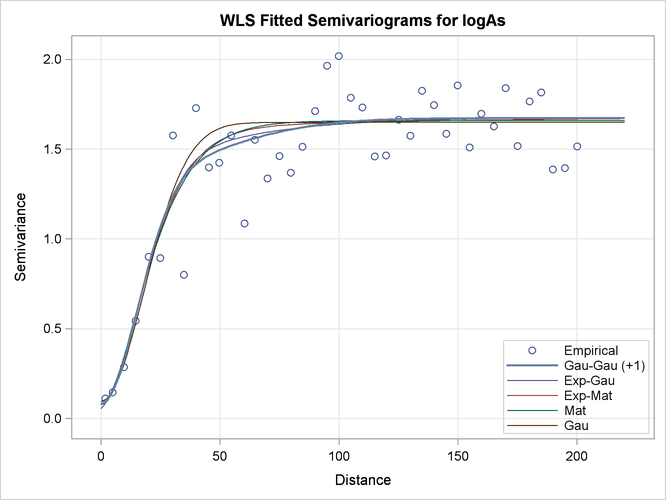
In the present example, all fitted models in the first five classes have very similar semivariograms. The selected Gaussian-Gaussian model seems to have a relatively larger range than the rest of the displayed models, but you can expect any of these models to exhibit a near-identical behavior in terms of spatial correlation. As a result, all models in the displayed classes are likely to lead to very similar output, if you proceed to use any of them for spatial prediction.
In that sense, semivariogram fitting is a partially subjective process, for which there might not exist only one single correct answer to solve your problem. In the context of the example, on one hand you might conclude that the selected Gaussian-Gaussian model is exactly sufficient to describe spatial correlation in the arsenic study. On the other hand, the similar performance of all models might prompt you to choose instead a more simple non-nested model for prediction like the Matérn or the Gaussian model.
Regardless of whether you might opt to sacrifice the statistically best fit (depending on your selected criteria) to simplicity, eventually you are the one to decide which approach serves your study optimally. The model fitting features of PROC VARIOGRAM offer you significant assistance so that you can assess your options efficiently.