The SEQDESIGN Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics
Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics -
Examples
 Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data
Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data - References
This example requests a two-sided design similar to Example 83.2, but with a nonbinding beta boundary. With a nonbinding acceptance boundary, the trial does not need to stop to accept the null hypothesis when a test statistic falls in the acceptance region at interim stages. The design maintains the specified Type I error level, but at the cost of increased sample size.
The following statements invoke the SEQDESIGN procedure and request a four-stage group sequential design with early stopping
to reject or accept ![]() :
:
ods graphics on;
proc seqdesign altref=0.15 errspend
;
NonbindingDesign: design nstages=4
method=obf
alt=upper
stop=both(betaboundary=nonbinding)
alpha=0.025 beta=0.10
;
samplesize model=twosamplefreq(nullprop=0.6 test=prop);
run;
ods graphics off;
The STOP=BOTH option specifies early stopping to reject or accept the null hypothesis, and the BETABOUNDARY=NONBINDING suboption requests the nonbinding beta boundary.
The “Design Information,” “Method Information,” and “Boundary Information” tables are displayed by default. The “Design Information” table in Output 83.13.1 displays design specifications and derived statistics such as power and maximum information. With a specified alternative
reference, ALTREF=0.15, the maximum information ![]() is derived.
is derived.
Output 83.13.1: Design Information
| Design Information | |
|---|---|
| Statistic Distribution | Normal |
| Boundary Scale | Standardized Z |
| Alternative Hypothesis | Upper |
| Early Stop | Accept(Nonbinding)/Reject Null |
| Method | O'Brien-Fleming |
| Boundary Key | Both |
| Alternative Reference | 0.15 |
| Number of Stages | 4 |
| Alpha (Binding Beta Boundary) | 0.02228 |
| Alpha (Nonbinding Beta Boundary) | 0.025 |
| Beta | 0.1 |
| Power | 0.9 |
| Max Information (Percent of Fixed Sample) | 110.7138 |
| Max Information | 517.0296 |
| Null Ref ASN (Percent of Fixed Sample) | 62.29796 |
| Alt Ref ASN (Percent of Fixed Sample) | 78.5392 |
With the BETABOUNDARY=NONBINDING option, there are two ways to compute the Type I error level: with or without the beta boundary. Alpha (Binding Beta Boundary) displays the Type I error level with the beta boundary, and Alpha (Nonbinding Beta Boundary) displays the Type I error level without the beta boundary.
The maximum information is the information level at the final stage of the group sequential trial. The Max Information (Percent Fixed-Sample) row displays the maximum information for the sequential design expressed as a percentage of the information for the corresponding fixed-sample design (which has a Type I error level 0.025). In Output 83.13.1, Max Information (Percent Fixed-Sample) is 110.71%, which means that the information needed for the group sequential trial is 10.71% more than the information needed for the corresponding fixed-sample design if the trial does not stop at any interim stage.
Compared to the corresponding design with a binding beta boundary, which has a Max Information (Percent Fixed-Sample) of 107.67% as displayed in Output 83.2.1, the nonbinding design requires a larger sample size if the trial proceeds to the final stage.
The “Method Information” table in Output 83.13.2 displays the values of ![]() and
and ![]() , which are the parameters for the O’Brien-Fleming method. The table also displays the drift parameter 3.4107, which is greater
than the drift parameter 3.3636 in the corresponding binding boundary design, as displayed in Output 83.2.2.
, which are the parameters for the O’Brien-Fleming method. The table also displays the drift parameter 3.4107, which is greater
than the drift parameter 3.3636 in the corresponding binding boundary design, as displayed in Output 83.2.2.
Output 83.13.2: Method Information
| Method Information | ||||||||
|---|---|---|---|---|---|---|---|---|
| Boundary | Method | Alpha | Beta | Unified Family | Alternative Reference |
Drift | ||
| Rho | Tau | C | ||||||
| Upper Alpha | O'Brien-Fleming | 0.02500 | . | 0.5 | 0 | 2.0243 | 0.15 | 3.410743 |
| Upper Beta | O'Brien-Fleming | . | 0.10000 | 0.5 | 0 | 1.38645 | 0.15 | 3.410743 |
The “Boundary Information” table in Output 83.13.3 displays information level, alternative reference, and boundary values at each stage. By default (or equivalently if you
specify BOUNDARYSCALE=STDZ), the alternative reference and boundary values are displayed with the standardized Z statistic scale. The resulting standardized alternative reference at stage k is given by ![]() , where
, where ![]() is the alternative reference and
is the alternative reference and ![]() is the information level at stage k, for k= 1, 2, 3, 4.
is the information level at stage k, for k= 1, 2, 3, 4.
Output 83.13.3: Boundary Information
| Boundary Information (Standardized Z Scale) Nonbinding Beta Boundary, Null Reference = 0 |
||||||
|---|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | ||||
| Information Level | Reference | Upper | ||||
| Proportion | Actual | N | Upper | Beta | Alpha | |
| 1 | 0.2500 | 129.2574 | 110.5151 | 1.70537 | -1.06752 | 4.04859 |
| 2 | 0.5000 | 258.5148 | 221.0302 | 2.41176 | 0.45103 | 2.86279 |
| 3 | 0.7500 | 387.7722 | 331.5452 | 2.95379 | 1.35286 | 2.33746 |
| 4 | 1.0000 | 517.0296 | 442.0603 | 3.41074 | 2.02430 | 2.02430 |
By default (or equivalently if you specify INFO=EQUAL), equally spaced information levels are used. With the derived maximum information, the actual information level at each stage is also displayed. With the SAMPLESIZE statement, the required sample size N is also displayed under the heading “Information Level.”
Note that with the standardized Z statistic scale, the rejection boundary values are identical to the boundary values that are derived in the corresponding
design with early stopping to reject ![]() .
.
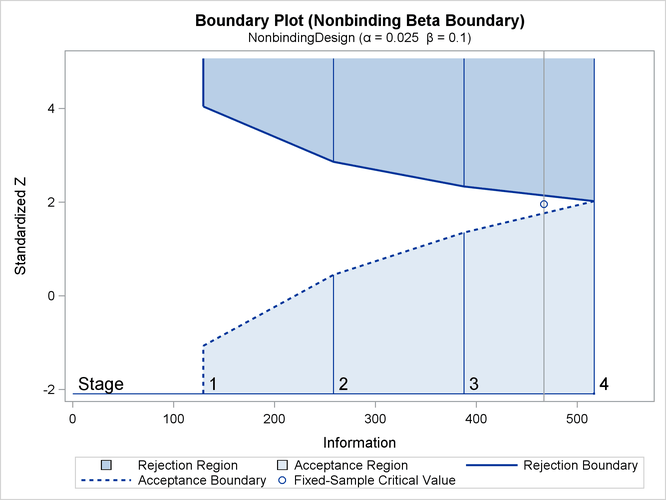
With ODS Graphics enabled, a detailed boundary plot with the rejection and acceptance regions is displayed, as shown in Output 83.13.4.
The horizontal axis indicates the information levels for the design. The stages are indicated by vertical lines with accompanying stage numbers. The boundary plot also displays the information level and the critical value for the corresponding fixed-sample design.
The “Error Spending Information (Nonbinding Beta Boundary)” table in Output 83.13.5 displays cumulative error spending at each stage for each boundary. With a nonbinding beta boundary, the ![]() spending at each stage is computed by using the
spending at each stage is computed by using the ![]() boundary only.
boundary only.
Output 83.13.5: Error Spending Information
| Error Spending Information (Nonbinding Beta Boundary) |
|||
|---|---|---|---|
| _Stage_ | Information Level |
Cumulative Error Spending | |
| Upper | |||
| Proportion | Beta | Alpha | |
| 1 | 0.2500 | 0.00278 | 0.00003 |
| 2 | 0.5000 | 0.02603 | 0.00211 |
| 3 | 0.7500 | 0.06343 | 0.01046 |
| 4 | 1.0000 | 0.10000 | 0.02500 |
The SEQDESIGN procedure derives the drift parameter ![]() , where
, where ![]() is the alternative reference and
is the alternative reference and ![]() is the maximum information. With the SAMPLESIZE statement, the maximum information is used to compute the required sample
size for the study.
is the maximum information. With the SAMPLESIZE statement, the maximum information is used to compute the required sample
size for the study.
The “Sample Size Summary” table in Output 83.13.6 displays parameters for the sample size computation. With the MODEL=TWOSAMPLEFREQ(NULLPROP=0.6 TEST=PROP) option in the SAMPLESIZE statement, the total sample size and expected sample sizes under the null and alternative hypotheses for testing the difference between two proportions are displayed.
Output 83.13.6: Sample Size Summary
| Sample Size Summary | |
|---|---|
| Test | Two-Sample Proportions |
| Null Proportion | 0.6 |
| Proportion (Group A) | 0.75 |
| Test Statistic | Z for Proportion |
| Reference Proportions | Alt Ref |
| Max Sample Size | 442.0603 |
| Expected Sample Size (Null Ref) | 248.7446 |
| Expected Sample Size (Alt Ref) | 313.5929 |
The “Sample Sizes (N)” table in Output 83.13.7 displays the required sample sizes at each stage, in both fractional and integer numbers. The derived fractional sample sizes are under the heading “Fractional N.” These sample sizes are rounded up to integers under the heading “Ceiling N.” As expected, the sample sizes in the table are larger than the corresponding sample sizes in the corresponding design with binding beta boundary.
Output 83.13.7: Derived Sample Sizes
| Sample Sizes (N) Two-Sample Z Test for Proportion Difference |
||||||||
|---|---|---|---|---|---|---|---|---|
| _Stage_ | Fractional N | Ceiling N | ||||||
| N | N(Grp 1) | N(Grp 2) | Information | N | N(Grp 1) | N(Grp 2) | Information | |
| 1 | 110.52 | 55.26 | 55.26 | 129.3 | 112 | 56 | 56 | 131.0 |
| 2 | 221.03 | 110.52 | 110.52 | 258.5 | 222 | 111 | 111 | 259.6 |
| 3 | 331.55 | 165.77 | 165.77 | 387.8 | 332 | 166 | 166 | 388.3 |
| 4 | 442.06 | 221.03 | 221.03 | 517.0 | 444 | 222 | 222 | 519.3 |