The CALIS Procedure
-
Overview

-
Getting Started

-
Syntax
 Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement
Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement -
Details
 Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics
Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis - References
LISMOD <var-lists> ;
where var-lists represent one or more of the following:
-
YVAR | YV | Y = var-list
-
XVAR | XV | X = var-list
-
ETAVAR | ETAV | ETA = var-list
-
XIVAR | XIV | XI | KSIVAR | KSIV | KSI = var-list
LISMOD stands for LISREL modeling, where LISREL is the program developed by Jöreskog and Sörbom (1988). Like the original implementation of LISREL, LISMOD uses a matrix specification interface. To complete the LISMOD specification, you might need to add as many MATRIX statements as needed, as shown in the following statement structure for the LISMOD model:
LISMOD
var-lists ;
MATRIX
matrix-name parameters-in-matrix ;
Repeat the MATRIX statement as needed
;
The matrix-name in the MATRIX statement should be one of the twelve model matrices in LISMOD, as listed in the following:
-
Matrices in the structural model: _ALPHA_, _KAPPA_, _BETA_, _GAMMA_, _PHI_, or _PSI_
-
Matrices in the measurement model for
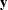 -variables: _NUY_, _LAMBDAY_, or _THETAY_
-variables: _NUY_, _LAMBDAY_, or _THETAY_
-
Matrices in the measurement model for
 -variables: _NUX_, _LAMBDAX_, or _THETAX_
-variables: _NUX_, _LAMBDAX_, or _THETAX_
See the section Model Matrices in the LISMOD Model for definitions of these matrices and their roles in the LISMOD modeling language. See the MATRIX statement for the details of parameter specification.
In the LISMOD statement, you can specify the following four lists of variables:
-
YVAR= list is for manifest variables
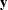 that are directly related to the endogenous latent variables
that are directly related to the endogenous latent variables 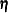 (eta). Variables in the list are called
(eta). Variables in the list are called 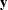 -variables.
-variables.
-
XVAR= list is for manifest variables
 that are directly related to the exogenous latent variables
that are directly related to the exogenous latent variables 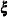 (xi or ksi). Variables in the list are called
(xi or ksi). Variables in the list are called  -variables.
-variables.
-
ETAVAR= list is for endogenous latent variables
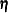 . Variables in the list are called
. Variables in the list are called 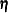 -variables.
-variables.
-
XIVAR= list is for exogenous latent variables
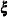 . Variables in the list are called
. Variables in the list are called 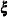 -variables.
-variables.
The order of variables in the lists of the LISMOD statement is used to define the variable order in rows and columns of the LISMOD model matrices.
Depending on the model of interest, you might not need to specify all the lists of variables. When some variable lists are not specified, the full model reduces to specialized submodels. However, to be a proper submodel in the LISMOD modeling language, it is necessary (but not sufficient) that at least one of the YVAR= or XVAR= lists is defined. See the section LISMOD Submodels for the details about LISMOD submodels that PROC CALIS can handle.
An example of a LISMOD model specification is shown as follows:
proc calis;
lismod xvar=x1-x3 yvar=y1-y6 xivar=xi etavar=eta1-eta2;
matrix _LAMBDAY_ [,1] = 1. load3 load4,
[,2] = 0. 0. 0. 1. load5 load6;
matrix _THETAY_ [1,1] = ey1-ey3,
[2,1] = cey;
matrix _LAMBDAX_ [,] = 1. load1 load2;
matrix _THETAX_ [1,1] = 3*ex;
matrix _GAMMA_ [,1] = beta1 beta2;
matrix _PHI_ [1,1] = phi;
matrix _PSI_ [1,1] = psi1-psi2;
run;
In this example, you have three ![]() -variables
-variables x1–x3, six ![]() -variables
-variables y1–y6, one ![]() -variable
-variable xi, and two ![]() -variables
-variables eta1–eta2. The numbers of variables in these lists define the dimensions of the LISMOD model matrices. For example, matrix _LAMBDAY_ is ![]() , with
, with y1–y6 as the row variables and eta1–eta2 as the column variables. Matrix _THETAX_ is ![]() , with
, with x1–x3 as the row and column variables. In the MATRIX statements, you specify parameters in the elements of the matrices. After
the matrix name, you specify in square brackets '[' and ']' the starting row and column numbers of the first element to be
parameterized. After the equal sign, you specify fixed or free parameters for the matrix elements.
Depending on how you specify the starting row and column numbers, the parameter specification might proceed differently. See
the
MATRIX statement
for a detailed description. In this example, the first specification of the parameters in the _LAMBDAY_ matrix starts from [,1]—meaning that it starts from the first column and proceeds downwards. As a result, the [1,1] element
is a fixed constant 1.0, the [2,1] element is a free parameter called load3, and the [3,1] element is a free parameter called load4. Similarly, in the second specification in the _LAMBDAY_ matrix, the [1,2], [2,2], [3,2], and [4,2] elements take constant values 0, 0, 0, and 1, respectively, and the [5,2] and
[6,2] elements are free parameters load5 and load6, respectively.
You can also use similar notation to specify the parameters of a row. For example, with the notation [2,] for the starting row and column numbers, specification proceeds to the left with the same second row in the matrix.
If you have specified both starting row and column numbers, such as those in the first specification in matrix _THETAY_, the parameter specification starts from [1,1] and proceeds to the next row and column numbers—that is [2,2], [3,3], and
so on. This results in specifying the diagonal elements of matrix _THETAY_ as free parameters ey1, ey2, and ey3.
With the notation [,], no starting row and column numbers are specified. Specification starts from the first valid element
in the matrix and proceeds row-wise for all valid elements in the matrix. For example, in the matrix _LAMBDAX_ statement, the [1,1] element of matrix _LAMBDAX_ is a fixed constant 1, and the [1,2] and [1,3] elements are free parameters load1 and load2, respectively.
It is important to understand the default parameters in the LISMOD model. First, if you know which parameters are default
free parameters, you can make your specification more efficient by omitting some specifications. For example, because all
variances and covariances among the exogenous ![]() -variables (excluding error terms) are free parameters by default, you do not need to specify them with MATRIX statement if
these variances and covariances are not constrained. Second, if you know which parameters are default fixed zero parameters,
you can specify your model accurately. For example, because all measurement errors in the LISMOD model are fixed zeros by
default, you must use the MATRIX statement to specify the covariances among the errors in the
-variables (excluding error terms) are free parameters by default, you do not need to specify them with MATRIX statement if
these variances and covariances are not constrained. Second, if you know which parameters are default fixed zero parameters,
you can specify your model accurately. For example, because all measurement errors in the LISMOD model are fixed zeros by
default, you must use the MATRIX statement to specify the covariances among the errors in the ![]() (_THETAX_) or
(_THETAX_) or ![]() (_THETAY_) matrices if you want to fit a model with some correlated measurement errors. See the section Default Parameters in the LISMOD Model for details about the default parameters of the LISMOD model.
(_THETAY_) matrices if you want to fit a model with some correlated measurement errors. See the section Default Parameters in the LISMOD Model for details about the default parameters of the LISMOD model.
This section assumes that you use a REFMODEL statement within the scope of a MODEL statement and that the reference model (or base model) is also a LISMOD model. The reference model is called the old model, and the model that refers to this old model is called the new model. If the new model is not intended to be an exact copy of the old model, you can use the extended LISMOD modeling language described in this section to make modifications within the scope of the MODEL statement for the new model. The syntax is similar to, but not exactly the same as, the ordinary LISMOD modeling language (see the section LISMOD Statement). The respecification syntax for a LISMOD model is shown as follows:
LISMOD
;
MATRIX
matrix-name parameters-in-matrix ;
Repeat the MATRIX statement as needed
;
First, in the respecification you should not put any variable lists in the LISMOD statement. The reason is that the parameter respecifications in the new model refer to the variable lists of the old model. Therefore, the variable lists in the new model are implicitly assumed to be exactly the same as those in the old model. Because of this, the LISMOD statement is entirely optional for the respecification in the new model.
Second, you can use MATRIX matrix-name statements to modify the old model by using the same syntax as in the LISMOD modeling language. The matrix-name can be one of the twelve possible LISMOD matrices. In addition, in the respecification syntax you can use the missing value '.' to drop a parameter specification from the old model.
The new model is formed by integrating with the old model in the following ways:
- Duplication:
-
If you do not specify in the new model a parameter location that exists in the old model, the old parameter specification is duplicated in the new model.
- Addition:
-
If you specify in the new model a parameter location that does not exist in the old model, the new parameter specification is used in the new model.
- Deletion:
-
If you specify in the new model a parameter location that also exists in the old model and the new parameter is denoted by the missing value '.', the old parameter specification is not copied into the new model.
- Replacement:
-
If you specify in the new model a parameter location that also exists in the old model and the new parameter is not denoted by the missing value '.', the new parameter specification replaces the old one in the new model.
For example, the following two-group analysis specifies Model 2 by referring to Model 1 in the REFMODEL statement:
proc calis;
group 1 / data=d1;
group 2 / data=d2;
model 1 / group=1;
lismod xvar=X1-X3 yvar=Y1-Y6 xivar=xi etavar=eta1-eta2;
matrix _LAMBDAY_ [,1] = 1. load3 load4,
[,2] = 0. 0. 0. 1. load5 load6;
matrix _THETAY_ [1,1] = ey1-ey3,
[2,1] = cey;
matrix _LAMBDAX_ [,] = 1. load1 load2;
matrix _THETAX_ [1,1] = 3*ex;
matrix _GAMMA_ [,1] = beta1 beta2;
matrix _PHI_ [1,1] = phi;
matrix _PSI_ [1,1] = psi1-psi2;
model 2 / group=2;
refmodel 1;
matrix _THETAY_ [2,1] = .;
matrix _THETAX_ [1,1] = ex1-ex3;
matrix _BETA_ [2,1] = beta;
run;
In this example, Model 2 is the new model which refers to the old model, Model 1. It illustrates the four types of model integration:
-
Duplication: All parameter locations and specifications in the old model are duplicated in the new model, except for the [2,1] element in matrix _THETAY_ and the diagonal of matrix _THETAX_, which are modified in the new model.
-
Addition: The _BETA_[2,1] parameter location is added with a new parameter
betain the new model. This indicates that eta1 is a predictor variable of eta2 in the new model, but not in the old model. -
Deletion: Because the missing value '.' is used for the parameter value, the _THETAY_[2,1] parameter location is no longer defined as a free parameter in the new model. In the old model, the same location is defined by the free parameter
cey. -
Replacement: The diagonal elements of the _THETAX_ matrix in the new model are now defined by three distinct parameters
ex1–ex3. This replaces the old specification where a single constrained parameterexis applied to all the diagonal elements in the _THETAX_ matrix.