The CALIS Procedure
-
Overview

-
Getting Started

-
Syntax
 Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement
Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement -
Details
 Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics
Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis - References
Standardized solutions are useful when you want to compare parameter values that are measured on quite different scales. PROC CALIS provides standardized solutions routinely. In standardizing a solution, parameters are classified into five groups:
-
path coefficients, regression coefficients, or direct effects With each parameter
 in this group, there is an associated outcome variable and a predictor variable. Denote the predicted variance of the outcome
variable by
in this group, there is an associated outcome variable and a predictor variable. Denote the predicted variance of the outcome
variable by 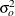 and the variance of the predictor variable by
and the variance of the predictor variable by 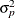 , the standardized parameter
, the standardized parameter 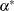 is:
is:
![\[ \alpha ^* = \alpha \frac{\sigma _ p}{\sigma _ o} \]](images/statug_calis0848.png)
-
fixed ones for the path coefficients attached to error or disturbance terms These fixed values are unchanged in standardization.
-
variances and covariances among exogenous variables, excluding errors and disturbances Let
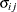 be the covariance between variables i and j. In this notation,
be the covariance between variables i and j. In this notation, 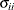 is the variance of variable i. The standardized covariance
is the variance of variable i. The standardized covariance 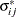 is:
is:
![\[ \sigma _{ij}^* = \frac{\sigma _{ij}}{{\sqrt {\sigma _{ii} \sigma _{jj}}}} \]](images/statug_calis0852.png)
When
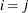 ,
, 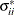 takes the value of 1 for all i. Also,
takes the value of 1 for all i. Also, 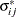 is the correlation between the ith and jth variables.
is the correlation between the ith and jth variables.
-
variances and covariances among errors or disturbances Denote the error covariance parameter as
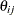 so that
so that 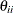 represents the variance parameter of error variable i. Associated with each error or disturbance variable i is a unique outcome variable. Let the variance of such an outcome variable be
represents the variance parameter of error variable i. Associated with each error or disturbance variable i is a unique outcome variable. Let the variance of such an outcome variable be 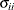 . In the standardized solution, the error covariance
. In the standardized solution, the error covariance 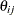 is rescaled as:
is rescaled as:
![\[ \theta _{ij}^* = \frac{\theta _{ij}}{{\sqrt {\sigma _{ii} \sigma _{jj}}}} \]](images/statug_calis0857.png)
Notice that when
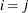 ,
, 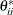 is not standardized to 1 in general. In fact, the error (disturbance) variance is simply rescaled by the reciprocal of the
variance of the associated dependent variable. As a result, the rescaled error (disturbance) variance represents the proportion
of variation of the dependent variable due to the unsystematic source. By the same token,
is not standardized to 1 in general. In fact, the error (disturbance) variance is simply rescaled by the reciprocal of the
variance of the associated dependent variable. As a result, the rescaled error (disturbance) variance represents the proportion
of variation of the dependent variable due to the unsystematic source. By the same token, 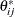 does not represent the correlation between errors i and j. It is a rescaled covariance of the errors involved.
does not represent the correlation between errors i and j. It is a rescaled covariance of the errors involved.
-
intercepts and means of variablesThese parameters are fixed zeros in the standardized solution.
While formulas for the standardized solution are useful in computing the parameter values in the standardized solution, it is conceptually more useful to explain how variables are being transformed in the standardization process. The following provides a summary of the transformation process:
-
Observed and latent variables, excluding errors or disturbances, are centered and then divided by their corresponding standard deviations. Therefore, in the standardized solution, all these variables will have variance equal to 1. In other words, these variables are truly standardized.
-
Errors or disturbances are divided by the standard deviations of the corresponding outcome variables. In the standardized solution, these variables will not have variance equal to 1 in general. However, the rescaled error variances represent the proportion of unexplained or unsystematic variance of the corresponding outcome variables. Therefore, errors or disturbances in the standardized solution are simply rescaled but not standardized.
Standardized total, direct, and indirect effects are computed using formulas presented in the section Total, Direct, and Indirect Effects, but with the standardized parameter values substituted into the formulas.
Although parameter values associated with different scales are made more comparable in the standardized solution, a precaution should be mentioned. In the standardized solution, the original constraints on parameters in the unstandardized solution are usually lost. These constraints, however, might underscore some important theoretical position that needs to be maintained in the model. Destroying these constraints in the standardized solution means that interpretations or comparisons of parameter values in the standardized solution are made without maintaining the original theoretical position. You must judge whether such a departure from the original constraints poses conceptual difficulties for interpreting the standardized solution.