The PHREG Procedure
- Overview
-
Getting Started
-
Syntax
PROC PHREG Statement ASSESS Statement BASELINE Statement BAYES Statement BY Statement CLASS Statement CONTRAST Statement EFFECT Statement ESTIMATE Statement FREQ Statement HAZARDRATIO Statement ID Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement Programming Statements RANDOM Statement STRATA Statement SLICE Statement STORE Statement TEST Statement WEIGHT Statement
-
Details
Failure Time Distribution Time and CLASS Variables Usage Partial Likelihood Function for the Cox Model Counting Process Style of Input Left-Truncation of Failure Times The Multiplicative Hazards Model The Frailty Model Hazard Ratios Specifics for Classical Analysis Specifics for Bayesian Analysis Computational Resources Input and Output Data Sets Displayed Output ODS Table Names ODS Graphics
-
Examples
Stepwise Regression Best Subset Selection Modeling with Categorical Predictors Firth’s Correction for Monotone Likelihood Conditional Logistic Regression for m:n Matching Model Using Time-Dependent Explanatory Variables Time-Dependent Repeated Measurements of a Covariate Survivor Function Estimates for Specific Covariate Values Analysis of Residuals Analysis of Recurrent Events Data Analysis of Clustered Data Model Assessment Using Cumulative Sums of Martingale Residuals Bayesian Analysis of the Cox Model Bayesian Analysis of Piecewise Exponential Model
- References
| The Multiplicative Hazards Model |
Consider a set of 
subjects such that the counting process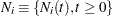 
for the 
th subject represents the number of observed events experienced over time 
. The sample paths of the process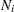 
are step functions with jumps of size 
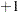, with 
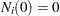. Let 
denote the vector of unknown regression coefficients. The multiplicative hazards function 
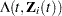for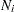 
is given by
 |
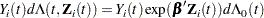where
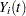indicates whether the th subject is at risk at time (specifically, 
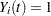if at risk and 
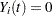otherwise) 
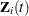is the vector of explanatory variables for the th subject at time 
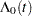is an unspecified baseline hazard function
Refer to Fleming and Harrington (1991) and Andersen et al. (1992). The Cox model is a special case of this multiplicative hazards model, where 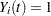until the first event or censoring, and 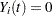thereafter.
The partial likelihood for independent triplets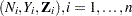 
, has the form
 |
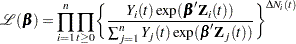where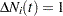 
if 
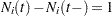, and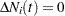 
otherwise.