The LOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC LOGISTIC Statement BY Statement CLASS Statement CONTRAST Statement EFFECT Statement EFFECTPLOT Statement ESTIMATE Statement EXACT Statement EXACTOPTIONS Statement FREQ Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement ODDSRATIO Statement OUTPUT Statement ROC Statement ROCCONTRAST Statement SCORE Statement SLICE Statement STORE Statement STRATA Statement TEST Statement UNITS Statement WEIGHT Statement
PROC LOGISTIC Statement BY Statement CLASS Statement CONTRAST Statement EFFECT Statement EFFECTPLOT Statement ESTIMATE Statement EXACT Statement EXACTOPTIONS Statement FREQ Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement ODDSRATIO Statement OUTPUT Statement ROC Statement ROCCONTRAST Statement SCORE Statement SLICE Statement STORE Statement STRATA Statement TEST Statement UNITS Statement WEIGHT Statement -
Details
 Missing Values Response Level Ordering Link Functions and the Corresponding Distributions Determining Observations for Likelihood Contributions Iterative Algorithms for Model Fitting Convergence Criteria Existence of Maximum Likelihood Estimates Effect-Selection Methods Model Fitting Information Generalized Coefficient of Determination Score Statistics and Tests Confidence Intervals for Parameters Odds Ratio Estimation Rank Correlation of Observed Responses and Predicted Probabilities Linear Predictor, Predicted Probability, and Confidence Limits Classification Table Overdispersion The Hosmer-Lemeshow Goodness-of-Fit Test Receiver Operating Characteristic Curves Testing Linear Hypotheses about the Regression Coefficients Regression Diagnostics Scoring Data Sets Conditional Logistic Regression Exact Conditional Logistic Regression Input and Output Data Sets Computational Resources Displayed Output ODS Table Names ODS Graphics
Missing Values Response Level Ordering Link Functions and the Corresponding Distributions Determining Observations for Likelihood Contributions Iterative Algorithms for Model Fitting Convergence Criteria Existence of Maximum Likelihood Estimates Effect-Selection Methods Model Fitting Information Generalized Coefficient of Determination Score Statistics and Tests Confidence Intervals for Parameters Odds Ratio Estimation Rank Correlation of Observed Responses and Predicted Probabilities Linear Predictor, Predicted Probability, and Confidence Limits Classification Table Overdispersion The Hosmer-Lemeshow Goodness-of-Fit Test Receiver Operating Characteristic Curves Testing Linear Hypotheses about the Regression Coefficients Regression Diagnostics Scoring Data Sets Conditional Logistic Regression Exact Conditional Logistic Regression Input and Output Data Sets Computational Resources Displayed Output ODS Table Names ODS Graphics -
Examples
 Stepwise Logistic Regression and Predicted Values Logistic Modeling with Categorical Predictors Ordinal Logistic Regression Nominal Response Data: Generalized Logits Model Stratified Sampling Logistic Regression Diagnostics ROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence Limits Comparing Receiver Operating Characteristic Curves Goodness-of-Fit Tests and Subpopulations Overdispersion Conditional Logistic Regression for Matched Pairs Data Firth’s Penalized Likelihood Compared with Other Approaches Complementary Log-Log Model for Infection Rates Complementary Log-Log Model for Interval-Censored Survival Times Scoring Data Sets Using the LSMEANS Statement
Stepwise Logistic Regression and Predicted Values Logistic Modeling with Categorical Predictors Ordinal Logistic Regression Nominal Response Data: Generalized Logits Model Stratified Sampling Logistic Regression Diagnostics ROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence Limits Comparing Receiver Operating Characteristic Curves Goodness-of-Fit Tests and Subpopulations Overdispersion Conditional Logistic Regression for Matched Pairs Data Firth’s Penalized Likelihood Compared with Other Approaches Complementary Log-Log Model for Infection Rates Complementary Log-Log Model for Interval-Censored Survival Times Scoring Data Sets Using the LSMEANS Statement - References
Example 53.7 ROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence Limits
This example plots an ROC curve, estimates a customized odds ratio, produces the traditional goodness-of-fit analysis, displays the generalized 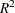 measures for the fitted model, calculates the normal confidence intervals for the regression parameters, and produces a display of the probability function and prediction curves for the fitted model. The data consist of three variables: n (number of subjects in the sample), disease (number of diseased subjects in the sample), and age (age for the sample). A linear logistic regression model is used to study the effect of age on the probability of contracting the disease. The statements to produce the data set and perform the analysis are as follows:
measures for the fitted model, calculates the normal confidence intervals for the regression parameters, and produces a display of the probability function and prediction curves for the fitted model. The data consist of three variables: n (number of subjects in the sample), disease (number of diseased subjects in the sample), and age (age for the sample). A linear logistic regression model is used to study the effect of age on the probability of contracting the disease. The statements to produce the data set and perform the analysis are as follows:
data Data1; input disease n age; datalines; 0 14 25 0 20 35 0 19 45 7 18 55 6 12 65 17 17 75 ;
ods graphics on;
proc logistic data=Data1 plots(only)=roc(id=obs);
model disease/n=age / scale=none
clparm=wald
clodds=pl
rsquare;
units age=10;
effectplot;
run;
ods graphics off;
The option SCALE=NONE is specified to produce the deviance and Pearson goodness-of-fit analysis without adjusting for overdispersion. The RSQUARE option is specified to produce generalized 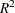 measures of the fitted model. The CLPARM=WALD option is specified to produce the Wald confidence intervals for the regression parameters. The UNITS statement is specified to produce customized odds ratio estimates for a change of 10 years in the age variable, and the CLODDS=PL option is specified to produce profile-likelihood confidence limits for the odds ratio. The PLOTS= option with ODS Graphics enabled produces a graphical display of the ROC curve, and the EFFECTPLOT statement displays the model fit.
measures of the fitted model. The CLPARM=WALD option is specified to produce the Wald confidence intervals for the regression parameters. The UNITS statement is specified to produce customized odds ratio estimates for a change of 10 years in the age variable, and the CLODDS=PL option is specified to produce profile-likelihood confidence limits for the odds ratio. The PLOTS= option with ODS Graphics enabled produces a graphical display of the ROC curve, and the EFFECTPLOT statement displays the model fit.
The results in Output 53.7.1 show that the deviance and Pearson statistics indicate no lack of fit in the model.
| Deviance and Pearson Goodness-of-Fit Statistics | ||||
|---|---|---|---|---|
| Criterion | Value | DF | Value/DF | Pr > ChiSq |
| Deviance | 7.7756 | 4 | 1.9439 | 0.1002 |
| Pearson | 6.6020 | 4 | 1.6505 | 0.1585 |
Output 53.7.2 shows that the R-square for the model is 0.74. The odds of an event increases by a factor of 7.9 for each 10-year increase in age.
| Model Fit Statistics | |||
|---|---|---|---|
| Criterion | Intercept Only |
Intercept and Covariates |
With Constant |
| AIC | 124.173 | 52.468 | 18.075 |
| SC | 126.778 | 57.678 | 23.285 |
| -2 Log L | 122.173 | 48.468 | 14.075 |
| R-Square | 0.5215 | Max-rescaled R-Square | 0.7394 |
|---|
| Testing Global Null Hypothesis: BETA=0 | |||
|---|---|---|---|
| Test | Chi-Square | DF | Pr > ChiSq |
| Likelihood Ratio | 73.7048 | 1 | <.0001 |
| Score | 55.3274 | 1 | <.0001 |
| Wald | 23.3475 | 1 | <.0001 |
| Analysis of Maximum Likelihood Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
Wald Chi-Square |
Pr > ChiSq |
| Intercept | 1 | -12.5016 | 2.5555 | 23.9317 | <.0001 |
| age | 1 | 0.2066 | 0.0428 | 23.3475 | <.0001 |
| Association of Predicted Probabilities and Observed Responses |
|||
|---|---|---|---|
| Percent Concordant | 92.6 | Somers' D | 0.906 |
| Percent Discordant | 2.0 | Gamma | 0.958 |
| Percent Tied | 5.4 | Tau-a | 0.384 |
| Pairs | 2100 | c | 0.953 |
| Parameter Estimates and Wald Confidence Intervals |
|||
|---|---|---|---|
| Parameter | Estimate | 95% Confidence Limits | |
| Intercept | -12.5016 | -17.5104 | -7.4929 |
| age | 0.2066 | 0.1228 | 0.2904 |
| Odds Ratio Estimates and Profile-Likelihood Confidence Intervals |
||||
|---|---|---|---|---|
| Effect | Unit | Estimate | 95% Confidence Limits | |
| age | 10.0000 | 7.892 | 3.881 | 21.406 |
Since ODS Graphics is enabled, a graphical display of the ROC curve is produced as shown in Output 53.7.3.
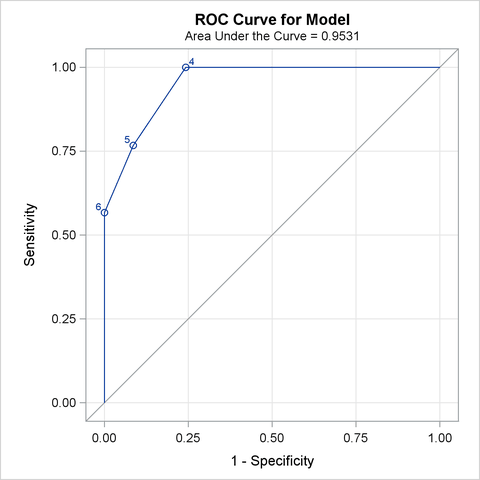
Note that the area under the ROC curve is estimated by the statistic c in the "Association of Predicted Probabilities and Observed Responses" table. In this example, the area under the ROC curve is 0.953.
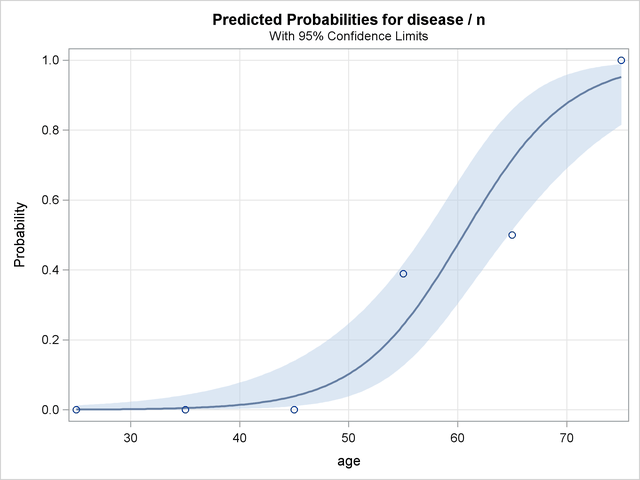
Since there is only one continuous covariate and since ODS Graphics is enabled, the EFFECTPLOT statement produces a graphical display of the predicted probability curve with bounding 95% confidence limits as shown in Output 53.7.4.