| The LOGISTIC Procedure |
Example 51.3 Ordinal Logistic Regression
Consider a study of the effects on taste of various cheese additives. Researchers tested four cheese additives and obtained 52 response ratings for each additive. Each response was measured on a scale of nine categories ranging from strong dislike (1) to excellent taste (9). The data, given in McCullagh and Nelder (1989, p. 175) in the form of a two-way frequency table of additive by rating, are saved in the data set Cheese by using the following program. The variable y contains the response rating. The variable Additive specifies the cheese additive (1, 2, 3, or 4). The variable freq gives the frequency with which each additive received each rating.
data Cheese;
do Additive = 1 to 4;
do y = 1 to 9;
input freq @@;
output;
end;
end;
label y='Taste Rating';
datalines;
0 0 1 7 8 8 19 8 1
6 9 12 11 7 6 1 0 0
1 1 6 8 23 7 5 1 0
0 0 0 1 3 7 14 16 11
;
The response variable y is ordinally scaled. A cumulative logit model is used to investigate the effects of the cheese additives on taste. The following statements invoke PROC LOGISTIC to fit this model with y as the response variable and three indicator variables as explanatory variables, with the fourth additive as the reference level. With this parameterization, each Additive parameter compares an additive to the fourth additive. The COVB option displays the estimated covariance matrix. The ODDSRATIO statement computes odds ratios for all combinations of the Additive levels. The PLOTS option produces a graphical display of the odds ratios, and the EFFECTPLOT statement displays the predicted probabilities.
ods graphics on; proc logistic data=Cheese plots(only)=oddsratio(range=clip); freq freq; class Additive (param=ref ref='4'); model y=Additive / covb; oddsratio Additive; effectplot / individual polybar; title 'Multiple Response Cheese Tasting Experiment'; run; ods graphics off;
The "Response Profile" table in Output 51.3.1 shows that the strong dislike (y=1) end of the rating scale is associated with lower Ordered Values in the "Response Profile" table; hence the probability of disliking the additives is modeled.
The score chi-square for testing the proportional odds assumption is 17.287, which is not significant with respect to a chi-square distribution with 21 degrees of freedom  . This indicates that the proportional odds assumption is reasonable. The positive value (1.6128) for the parameter estimate for Additive1 indicates a tendency toward the lower-numbered categories of the first cheese additive relative to the fourth. In other words, the fourth additive tastes better than the first additive. The second and third additives are both less favorable than the fourth additive. The relative magnitudes of these slope estimates imply the preference ordering: fourth, first, third, second.
. This indicates that the proportional odds assumption is reasonable. The positive value (1.6128) for the parameter estimate for Additive1 indicates a tendency toward the lower-numbered categories of the first cheese additive relative to the fourth. In other words, the fourth additive tastes better than the first additive. The second and third additives are both less favorable than the fourth additive. The relative magnitudes of these slope estimates imply the preference ordering: fourth, first, third, second.
| Multiple Response Cheese Tasting Experiment |
| Model Information | ||
|---|---|---|
| Data Set | WORK.CHEESE | |
| Response Variable | y | Taste Rating |
| Number of Response Levels | 9 | |
| Frequency Variable | freq | |
| Model | cumulative logit | |
| Optimization Technique | Fisher's scoring | |
| Number of Observations Read | 36 |
|---|---|
| Number of Observations Used | 28 |
| Sum of Frequencies Read | 208 |
| Sum of Frequencies Used | 208 |
| Response Profile | ||
|---|---|---|
| Ordered Value |
y | Total Frequency |
| 1 | 1 | 7 |
| 2 | 2 | 10 |
| 3 | 3 | 19 |
| 4 | 4 | 27 |
| 5 | 5 | 41 |
| 6 | 6 | 28 |
| 7 | 7 | 39 |
| 8 | 8 | 25 |
| 9 | 9 | 12 |
| Note: | 8 observations having nonpositive frequencies or weights were excluded since they do not contribute to the analysis. |
| Class Level Information | ||||
|---|---|---|---|---|
| Class | Value | Design Variables | ||
| Additive | 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | |
| 3 | 0 | 0 | 1 | |
| 4 | 0 | 0 | 0 | |
| Model Fit Statistics | ||
|---|---|---|
| Criterion | Intercept Only |
Intercept and Covariates |
| AIC | 875.802 | 733.348 |
| SC | 902.502 | 770.061 |
| -2 Log L | 859.802 | 711.348 |
| Testing Global Null Hypothesis: BETA=0 | |||
|---|---|---|---|
| Test | Chi-Square | DF | Pr > ChiSq |
| Likelihood Ratio | 148.4539 | 3 | <.0001 |
| Score | 111.2670 | 3 | <.0001 |
| Wald | 115.1504 | 3 | <.0001 |
| Analysis of Maximum Likelihood Estimates | ||||||
|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
Wald Chi-Square |
Pr > ChiSq | |
| Intercept | 1 | 1 | -7.0801 | 0.5624 | 158.4851 | <.0001 |
| Intercept | 2 | 1 | -6.0249 | 0.4755 | 160.5500 | <.0001 |
| Intercept | 3 | 1 | -4.9254 | 0.4272 | 132.9484 | <.0001 |
| Intercept | 4 | 1 | -3.8568 | 0.3902 | 97.7087 | <.0001 |
| Intercept | 5 | 1 | -2.5205 | 0.3431 | 53.9704 | <.0001 |
| Intercept | 6 | 1 | -1.5685 | 0.3086 | 25.8374 | <.0001 |
| Intercept | 7 | 1 | -0.0669 | 0.2658 | 0.0633 | 0.8013 |
| Intercept | 8 | 1 | 1.4930 | 0.3310 | 20.3439 | <.0001 |
| Additive | 1 | 1 | 1.6128 | 0.3778 | 18.2265 | <.0001 |
| Additive | 2 | 1 | 4.9645 | 0.4741 | 109.6427 | <.0001 |
| Additive | 3 | 1 | 3.3227 | 0.4251 | 61.0931 | <.0001 |
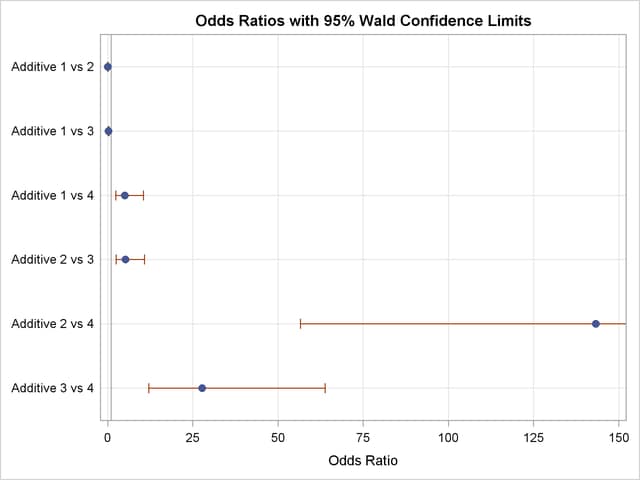
The odds ratio results in Output 51.3.2 show the preferences more clearly. For example, the "Additive 1 vs 4" odds ratio says that the first additive has 5.017 times the odds of receiving a lower score than the fourth additive; that is, the first additive is 5.017 times more likely than the fourth additive to receive a lower score. Output 51.3.3 displays the odds ratios graphically; the range of the confidence limits is truncated by the RANGE=CLIP option, so you can see that "1" is not contained in any of the intervals.
The estimated covariance matrix of the parameters is displayed in Output 51.3.4.
| Estimated Covariance Matrix | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | Intercept_1 | Intercept_2 | Intercept_3 | Intercept_4 | Intercept_5 | Intercept_6 | Intercept_7 | Intercept_8 | Additive1 | Additive2 | Additive3 |
| Intercept_1 | 0.316291 | 0.219581 | 0.176278 | 0.147694 | 0.114024 | 0.091085 | 0.057814 | 0.041304 | -0.09419 | -0.18686 | -0.13565 |
| Intercept_2 | 0.219581 | 0.226095 | 0.177806 | 0.147933 | 0.11403 | 0.091081 | 0.057813 | 0.041304 | -0.09421 | -0.18161 | -0.13569 |
| Intercept_3 | 0.176278 | 0.177806 | 0.182473 | 0.148844 | 0.114092 | 0.091074 | 0.057807 | 0.0413 | -0.09427 | -0.1687 | -0.1352 |
| Intercept_4 | 0.147694 | 0.147933 | 0.148844 | 0.152235 | 0.114512 | 0.091109 | 0.05778 | 0.041277 | -0.09428 | -0.14717 | -0.13118 |
| Intercept_5 | 0.114024 | 0.11403 | 0.114092 | 0.114512 | 0.117713 | 0.091821 | 0.057721 | 0.041162 | -0.09246 | -0.11415 | -0.11207 |
| Intercept_6 | 0.091085 | 0.091081 | 0.091074 | 0.091109 | 0.091821 | 0.09522 | 0.058312 | 0.041324 | -0.08521 | -0.09113 | -0.09122 |
| Intercept_7 | 0.057814 | 0.057813 | 0.057807 | 0.05778 | 0.057721 | 0.058312 | 0.07064 | 0.04878 | -0.06041 | -0.05781 | -0.05802 |
| Intercept_8 | 0.041304 | 0.041304 | 0.0413 | 0.041277 | 0.041162 | 0.041324 | 0.04878 | 0.109562 | -0.04436 | -0.0413 | -0.04143 |
| Additive1 | -0.09419 | -0.09421 | -0.09427 | -0.09428 | -0.09246 | -0.08521 | -0.06041 | -0.04436 | 0.142715 | 0.094072 | 0.092128 |
| Additive2 | -0.18686 | -0.18161 | -0.1687 | -0.14717 | -0.11415 | -0.09113 | -0.05781 | -0.0413 | 0.094072 | 0.22479 | 0.132877 |
| Additive3 | -0.13565 | -0.13569 | -0.1352 | -0.13118 | -0.11207 | -0.09122 | -0.05802 | -0.04143 | 0.092128 | 0.132877 | 0.180709 |
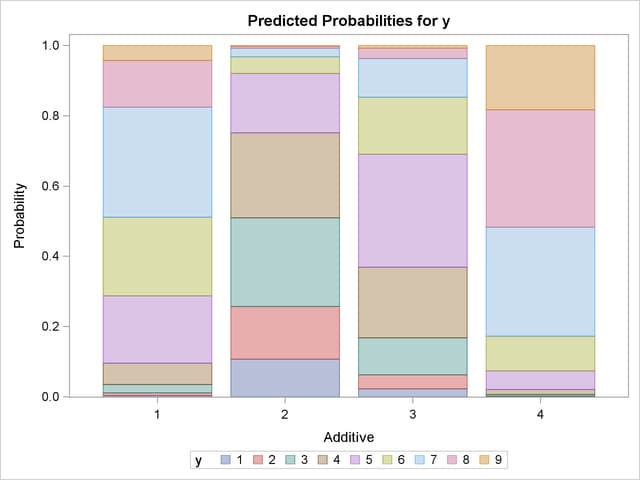
Output 51.3.5 displays the probability of each taste rating y within each additive. You can see that Additive=1 mostly receives ratings of 5 to 7, Additive=2 mostly receives ratings of 2 to 5, Additive=3 mostly receives ratings of 4 to 6, and Additive=4 mostly receives ratings of 7 to 9, which also confirms the previously discussed preference orderings.
Copyright © SAS Institute, Inc. All Rights Reserved.