| Introduction to Structural Equation Modeling with Latent Variables |
| Identification of Models |
Unfortunately, if you try to fit models of form B or form C without additional constraints, you cannot obtain unique estimates of the parameters. These models have four parameters (one coefficient and three variances). The covariance matrix of the observed variables  and
and 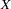 has only three elements that are free to vary, since Cov(
has only three elements that are free to vary, since Cov( ,
,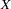 )=Cov(
)=Cov(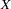 ,
, ). The covariance structure can, therefore, be expressed as three equations in four unknown parameters. Since there are fewer equations than unknowns, there are many different sets of values for the parameters that provide a solution for the equations. Such a model is said to be underidentified.
). The covariance structure can, therefore, be expressed as three equations in four unknown parameters. Since there are fewer equations than unknowns, there are many different sets of values for the parameters that provide a solution for the equations. Such a model is said to be underidentified.
If the number of parameters equals the number of free elements in the covariance matrix, then there might exist a unique set of parameter estimates that exactly reproduce the observed covariance matrix. In this case, the model is said to be just identified or saturated.
If the number of parameters is less than the number of free elements in the covariance matrix, there might exist no set of parameter estimates that reproduces the observed covariance matrix. In this case, the model is said to be overidentified. Various statistical criteria, such as maximum likelihood, can be used to choose parameter estimates that approximately reproduce the observed covariance matrix. If you use ML, GLS, or WLS estimation, PROC TCALIS can perform a statistical test of the goodness of fit of the model under the certain statistical assumptions.
If the model is just identified or overidentified, it is said to be identified. If you use ML, GLS, or WLS estimation for an identified model, PROC TCALIS can compute approximate standard errors for the parameter estimates. For underidentified models, PROC TCALIS obtains approximate standard errors by imposing additional constraints resulting from the use of a generalized inverse of the Hessian matrix.
You cannot guarantee that a model is identified simply by counting the parameters. For example, for any latent variable, you must specify a numeric value for the variance, or for some covariance involving the variable, or for a coefficient of the variable in at least one equation. Otherwise, the scale of the latent variable is indeterminate, and the model will be underidentified regardless of the number of parameters and the size of the covariance matrix. As another example, an exploratory factor analysis with two or more common factors is always underidentified because you can rotate the common factors without affecting the fit of the model.
PROC TCALIS can usually detect an underidentified model by computing the approximate covariance matrix of the parameter estimates and checking whether any estimate is linearly related to other estimates (Bollen 1989, pp. 248–250), in which case PROC TCALIS displays equations showing the linear relationships among the estimates. Another way to obtain empirical evidence regarding the identification of a model is to run the analysis several times with different initial estimates to see if the same final estimates are obtained.
Bollen (1989) provides detailed discussions of conditions for identification in a variety of models.
The following example is inspired by Fuller (1987, pp. 40–41). The hypothetical data are counts of two types of cells, cells forming rosettes and nucleated cells, in spleen samples. It is reasonable to assume that counts have a Poisson distribution; hence, the square roots of the counts should have a constant error variance of 0.25.
You can use PROC TCALIS to fit a model of form C to the square roots of the counts without constraints on the parameters, as displayed in the following statements:
data spleen;
input rosette nucleate;
sqrtrose=sqrt(rosette);
sqrtnucl=sqrt(nucleate);
datalines;
4 62
5 87
5 117
6 142
8 212
9 120
12 254
13 179
15 125
19 182
28 301
51 357
;
proc tcalis data=spleen;
lineqs sqrtrose = factrose + err_rose,
sqrtnucl = factnucl + err_nucl,
factrose = beta factnucl + disturb;
std err_rose = v_rose,
err_nucl = v_nucl,
factnucl = v_factnu,
disturb = 0;
run;
This model is underidentified. PROC TCALIS displays the following warning:
WARNING: Estimation problem not identified: More parameters to
estimate ( 4 ) than the total number of mean and
covariance elements ( 3 ).
Then it diagnoses the indeterminacy as follows:
NOTE: Covariance matrix for the estimates is not full rank.
NOTE: The variance of some parameter estimates is zero or
some parameter estimates are linearly related to other
parameter estimates as shown in the following equations:
v_rose = 0.207718 + 0.108978 * beta
+ 0.916873 * v_nucl
- 0.916873 * v_factnu
The constraint that the error variances equal 0.25 can be imposed by modifying the STD statement:
proc tcalis data=spleen;
lineqs sqrtrose = factrose + err_rose,
sqrtnucl = factnucl + err_nucl,
factrose = beta factnucl + disturb;
std err_rose = .25,
err_nucl = .25,
factnucl = v_factnu,
disturb = 0;
run;
This model is overidentified and the chi-square goodness-of-fit test yields a p-value of  , as displayed in Figure 17.2.
, as displayed in Figure 17.2.
| Fit Summary | ||
|---|---|---|
| Modeling Info | N Observations | 12 |
| N Variables | 2 | |
| N Moments | 3 | |
| N Parameters | 2 | |
| N Active Constraints | 0 | |
| Independence Model Chi-Square | 13.2732 | |
| Independence Model Chi-Square DF | 1 | |
| Absolute Index | Fit Function | 0.4775 |
| Chi-Square | 5.2522 | |
| Chi-Square DF | 1 | |
| Pr > Chi-Square | 0.0219 | |
| Z-Test of Wilson & Hilferty | 2.0375 | |
| Hoelter Critical N | 10 | |
| Root Mean Square Residual (RMSR) | 0.1785 | |
| Standardized RMSR (SRMSR) | 0.0745 | |
| Goodness of Fit Index (GFI) | 0.7274 | |
| Parsimony Index | Adjusted GFI (AGFI) | 0.1821 |
| Parsimonious GFI | 0.7274 | |
| RMSEA Estimate | 0.6217 | |
| RMSEA Lower 90% Confidence Limit | 0.1899 | |
| RMSEA Upper 90% Confidence Limit | 1.1869 | |
| Probability of Close Fit | 0.0237 | |
| ECVI Estimate | 0.9775 | |
| ECVI Lower 90% Confidence Limit | . | |
| ECVI Upper 90% Confidence Limit | 2.2444 | |
| Akaike Information Criterion | 3.2522 | |
| Bozdogan CAIC | 1.7673 | |
| Schwarz Bayesian Criterion | 2.7673 | |
| McDonald Centrality | 0.8376 | |
| Incremental Index | Bentler Comparative Fit Index | 0.6535 |
| Bentler-Bonett NFI | 0.6043 | |
| Bentler-Bonett Non-normed Index | 0.6535 | |
| Bollen Normed Index Rho1 | 0.6043 | |
| Bollen Non-normed Index Delta2 | 0.6535 | |
| James et al. Parsimonious NFI | 0.6043 | |
PROC TCALIS arranges the fit statistics according to their types: absolute, parsimony, and incremental. After displaying some important modeling information in the fit summary table, the absolute fit indices are printed. Absolute indices are those model fit statistics that assess the model fit without comparing to a "null" model. The most typical fit index of the this type is the chi-square fit statistic. Nonsignificance of the chi-square indicates good model fit. Other popular absolute fit indices include the root mean square residual (RMSR), the standardized RMSR (SRMSR), and the goodness-of-fit index (GFI). By convention, a good model should have an SRMSR smaller than 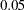 and a GFI larger than
and a GFI larger than 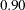 .
.
Parsimony indices are those fit indices that assess the model fit without comparing with a null model, but with the number of parameters in the model taking into account. These fit indices favor precise models. If two models have the same chi-square value for the same data set but have different number of parameters in the models, the model with fewer parameters will have a better parsimony fit statistic. The most popular parsimony index displayed in the table is perhaps the root mean squared error of approximation, or RMSEA (Steiger and Lind 1980). An RMSEA below 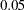 is recommended for a good model fit (Browne and Cudeck 1993). Another popular index in this category is the adjusted GFI (AGFI). By convention, an AGFI above
is recommended for a good model fit (Browne and Cudeck 1993). Another popular index in this category is the adjusted GFI (AGFI). By convention, an AGFI above 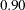 is required for a good model fit.
is required for a good model fit.
Finally, the incremental fit indices are those indices that measure model fit by comparing with a null model. A null model is usually the independence model that assumes the measured variables are all uncorrelated. The most popular incremental index is Bentler’s CFI. By convention, a CFI above 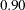 is required for a good model fit.
is required for a good model fit.
After the model fit summary, the parameter estimates are displayed in Figure 17.3.
Overall, the model does not provide a good fit. The sample size is so small that the p-value of the chi-square test should not be taken to be accurate, but to get a small p-value with such a small sample indicates it is possible that the model is seriously deficient. The deficiency could be due to any of the following:
The error variances are not both equal to 0.25.
The error terms are correlated with each other or with the true scores.
The observations are not independent.
There is a nonzero disturbance in the linear relation between factrose and factnucl.
The relation between factrose and factnucl is not linear.
The actual distributions are not adequately approximated by the multivariate normal distribution.
A simple and plausible modification to the model is to make the "disturbance term" disturb a real random variable with nonzero variance in the structural model. This can be done by giving the variance of disturb a parameter name in the STD statement, as shown in the following statements:
proc tcalis data=spleen;
lineqs sqrtrose = factrose + err_rose,
sqrtnucl = factnucl + err_nucl,
factrose = beta factnucl + disturb;
std err_rose = .25,
err_nucl = .25,
factnucl = v_factnu,
disturb = v_dist;
run;
In the STD statement, v_dist is now specified as a free variance parameter to be estimated. The parameter estimates are produced in Figure 17.4.
As shown in Figure 17.4, the variance of disturb is estimated at 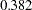 . Due to the inclusion of this new parameter, estimates for beta and v_factnu also shift a little bit from the previous analysis. Because this model is just identified or saturated, there are no degrees of freedom for the chi-square goodness-of-fit test.
. Due to the inclusion of this new parameter, estimates for beta and v_factnu also shift a little bit from the previous analysis. Because this model is just identified or saturated, there are no degrees of freedom for the chi-square goodness-of-fit test.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.