| Introduction to Structural Equation Modeling with Latent Variables |
Structural Equation Models and the LINEQS Modeling Language
Consider fitting a linear equation to two observed variables,  and
and 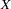 . Simple linear regression uses the model of a particular form, labeled for purposes of discussion, as model form A.
. Simple linear regression uses the model of a particular form, labeled for purposes of discussion, as model form A.
Model Form A
 |
with the following assumption:
 |
where  and
and  are coefficients to be estimated and
are coefficients to be estimated and  is an error term. If the values of
is an error term. If the values of 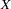 are fixed, the values of
are fixed, the values of  are assumed to be independent and identically distributed realizations of a normally distributed random variable with mean zero and variance Var(
are assumed to be independent and identically distributed realizations of a normally distributed random variable with mean zero and variance Var( ). If
). If 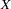 is a random variable,
is a random variable, 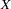 and
and  are assumed to have a bivariate normal distribution with zero correlation and variances Var(
are assumed to have a bivariate normal distribution with zero correlation and variances Var(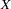 ) and Var(
) and Var( ), respectively. Under either set of assumptions, the usual formulas hold for the estimates of the coefficients and their standard errors (see
Chapter 4,
Introduction to Regression Procedures
).
), respectively. Under either set of assumptions, the usual formulas hold for the estimates of the coefficients and their standard errors (see
Chapter 4,
Introduction to Regression Procedures
).
In the REG or SYSLIN procedure, you would fit a simple linear regression model with a MODEL statement listing only the names of the manifest variables, as shown in the following statements:
proc reg;
model y = x;
run;
You can also fit this model with PROC TCALIS, but you must explicitly specify the error terms and the parameter name for the regression coefficient (except for the intercept, which is assumed to be present in each equation). The following specification in PROC TCALIS is equivalent to the preceding regression model:
proc tcalis;
lineqs
y = beta x + ey;
run;
where beta is the parameter name for the regression coefficient and ey is the error term of the equation. You do not need to type an "*" between beta and x to indicate the multiplication of the variable by the coefficient.
You might use other names for the parameters and the error terms, but there are rules to follow in the LINEQS model specification. The LINEQS statement uses the convention that the names of error terms begin with the letter E or e, disturbances (errors terms for latent variables) in equations begin with D or d, and other latent variables begin with F or f for "factor." Names of variables in the input SAS data set can, of course, begin with any letter.
Optionally, you can specify the variance parameters of exogenous variables explicitly by using the STD statement as follows:
proc tcalis;
lineqs
y = beta x + ey;
std
x = vx,
ey = vey;
run;
where vx and vey represent the variance of x and ey, respectively. Explicitly giving these variance parameters names would be useful when you need to set constraints on these parameters by referring to their names. In this simple case without constraints, however, naming these variance parameters is not necessary.
Although naming variance parameters for exogenous variables is optional, naming the regression coefficients when they should be free parameters is not. Consider the following statements:
proc tcalis;
lineqs
y = x + ey;
run;
In this specification, you leave out the regression coefficient beta from the preceding LINEQS model. Instead of being a parameter to estimate, the regression coefficient in this specification is a fixed constant 1.
In certain special situations where you need to specify a regression equation without an error term, you can explicitly set the variance of the error term to zero. For example, the following statements, in effect, will fit an equation without an error term:
proc tcalis;
lineqs
y = beta x + ey;
std
ey = 0;
run;
In this specification, the mean of the error term ey is presumably zero, as all error terms in the PROC TCALIS are set to have fixed zero means. Together with the zero variance specification for ey in the STD statement, ey is essentially a zero constant in the equation.
By default, PROC TCALIS analyzes the covariance matrix. This is exactly the opposite of PROC CALIS or PROC FACTOR, which analyzes the correlation matrix by default. Most applications that use PROC TCALIS should employ the default covariance structure analysis.
Since the analysis of covariance structures is based on modeling the covariance matrix and the covariance matrix contains no information about means, PROC TCALIS neglects the intercept parameter by default. To estimate the intercept, you can add the intercept term explicitly into the LINEQS statement. For example, the following statements fit a regression model with the estimation of the intercept alpha:
proc tcalis;
lineqs
y = alpha intercept + beta x + ey;
run;
In the LINEQS statement, intercept represents a "variable" with a constant value of 1; hence, the coefficient alpha is the intercept parameter. Notice that with the simultaneous analysis of mean and covariance structures, you have to provide either the raw data or the means and covariances in your input data set.
Other commonly used options in the PROC TCALIS statement include the following:
MODIFICATION to display model modification indices
NOBS to specify the number of observations
NOSE to suppress the display of approximate standard errors
RESIDUAL to display residual correlations or covariances
TOTEFF to display total and indirect effects
For ordinary unconstrained regression models, there is no reason to use PROC TCALIS instead of PROC REG. But suppose that the observed variables  and
and 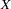 are contaminated by errors (especially measurement errors), and you want to estimate the linear relationship between their true, error-free scores. The model can be written in several forms. A model of form B is as follows.
are contaminated by errors (especially measurement errors), and you want to estimate the linear relationship between their true, error-free scores. The model can be written in several forms. A model of form B is as follows.
Model Form B
 |
 |
 |
|||
 |
 |
 |
with the following assumption:
 |
This model has two error terms,  and
and  , as well as another latent variable
, as well as another latent variable  representing the true value corresponding to the manifest variable
representing the true value corresponding to the manifest variable 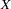 . The true value corresponding to
. The true value corresponding to  does not appear explicitly in this form of the model.
does not appear explicitly in this form of the model.
The assumption in model form B that the error terms and the latent variable  are jointly uncorrelated is of critical importance. This assumption must be justified on substantive grounds such as the physical properties of the measurement process. If this assumption is violated, the estimators might be severely biased and inconsistent.
are jointly uncorrelated is of critical importance. This assumption must be justified on substantive grounds such as the physical properties of the measurement process. If this assumption is violated, the estimators might be severely biased and inconsistent.
You can express model form B in the LINEQS statement as follows:
proc tcalis;
lineqs
y = beta fx + ey,
x = fx + ex;
std
fx = vfx,
ey = vey,
ex = vex;
run;
In this specification, you specify a variance for each of the latent variables in this model by using the STD statement. You can specify either a name, in which case the variance is considered a parameter to be estimated, or a number, in which case the variance is constrained to equal that numeric value. In this model, vfx, vey, and vex are variance parameters to estimate.
The variances of endogenous variables are predicted from the model and hence are not parameters. Covariances involving latent exogenous variables are assumed to be zero by default.
Fuller (1987, pp. 18–19) analyzes a data set from Voss (1969) involving corn yields ( ) and available soil nitrogen (
) and available soil nitrogen (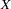 ) for which there is a prior estimate of the measurement error for soil nitrogen Var(
) for which there is a prior estimate of the measurement error for soil nitrogen Var( ) of 57. You can fit model form B with this constraint to the data by using the following statements:
) of 57. You can fit model form B with this constraint to the data by using the following statements:
data corn(type=cov);
input _type_ $ _name_ $ y x;
datalines;
n . 11 11
mean . 97.4545 70.6364
cov y 87.6727 .
cov x 104.8818 304.8545
;
proc tcalis data=corn;
lineqs y = beta fx + ey,
x = fx + ex;
std ex = 57,
fx = vfx,
ey = vey;
run;
In the STD statement, the variance of ex is given as the constant value 57. PROC TCALIS produces the estimates shown in Figure 17.1.
PROC TCALIS also displays information about the initial estimates that can be useful if there are optimization problems. If there are no optimization problems, the initial estimates are usually not of interest; they are not reproduced in the examples in this chapter.
You can write an equivalent model (labeled here as model form C) by using a latent variable  to represent the true value corresponding to
to represent the true value corresponding to  .
.
Model Form C
 |
 |
 |
|||
 |
 |
 |
|||
 |
 |
 |
with the following assumption:
 |
The first two equations express the observed variables in terms of a true score plus error; these two equations are called the measurement model. The third equation, expressing the relationship between the latent true-score variables, is called the structural or causal model. The decomposition of a model into a measurement model and a structural model (Keesling 1972; Wiley 1973; Jöreskog 1973) has been popularized by the program LISREL (Jöreskog and Sörbom 1988). The statements for fitting this model are shown in the following:
proc tcalis;
lineqs
y = fy + ey,
x = fx + ex,
fy = beta fx + dfy;
std
fx = vfx,
ey = vey,
ex = vex,
dfy = 0;
run;
As a syntactic requirement, each equation in the LINEQS statement should have an error term. As discussed before, because dfy has a fixed variance  in the STD statement, in effect, there is no error term in the structural equation with the outcome variable fy.
in the STD statement, in effect, there is no error term in the structural equation with the outcome variable fy.
You do not need to include the variance of  in the STD statement because the variance of
in the STD statement because the variance of  is determined by the structural model in terms of the variance of
is determined by the structural model in terms of the variance of  —that is, Var(
—that is, Var( )=
)= Var(
Var( ).
).
Correlations or covariances involving endogenous variables are derived from the model. For example, the structural equation in model form C implies that  and
and  are correlated unless
are correlated unless  is zero. In all of the models discussed so far, the latent exogenous variables are assumed to be jointly uncorrelated. For example, in model form C,
is zero. In all of the models discussed so far, the latent exogenous variables are assumed to be jointly uncorrelated. For example, in model form C,  ,
,  , and
, and  are assumed to be uncorrelated. If you want to specify a model in which
are assumed to be uncorrelated. If you want to specify a model in which  and
and  , say, are correlated, you can use the COV statement to specify the numeric value of the covariance Cov(
, say, are correlated, you can use the COV statement to specify the numeric value of the covariance Cov( ,
,  ) between
) between  and
and  , or you can specify a name to make the covariance a parameter to be estimated. For example:
, or you can specify a name to make the covariance a parameter to be estimated. For example:
proc tcalis;
lineqs
y = fy + ey,
x = fx + ex,
fy = beta fx + dfy;
std
fx = vfx,
ey = vey,
ex = vex,
dfy = 0;
cov
ey ex = ceyex;
run;
This COV statement specifies that the covariance between ey and ex is a parameter named ceyex. All covariances that are not listed in the COV statement and that are not determined by the model are assumed to be zero. If the model contained two or more manifest exogenous variables, their covariances would be set as free parameters by default.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.