The RELIABILITY Procedure
- Overview
-
Getting Started
 Analysis of Right-Censored Data from a Single PopulationWeibull Analysis Comparing Groups of DataAnalysis of Accelerated Life Test DataWeibull Analysis of Interval Data with Common Inspection ScheduleLognormal Analysis with Arbitrary CensoringRegression ModelingRegression Model with Nonconstant ScaleRegression Model with Two Independent VariablesWeibull Probability Plot for Two Combined Failure ModesAnalysis of Recurrence Data on RepairsComparison of Two Samples of Repair DataAnalysis of Interval Age Recurrence DataAnalysis of Binomial DataThree-Parameter WeibullParametric Model for Recurrent Events DataParametric Model for Interval Recurrent Events Data
Analysis of Right-Censored Data from a Single PopulationWeibull Analysis Comparing Groups of DataAnalysis of Accelerated Life Test DataWeibull Analysis of Interval Data with Common Inspection ScheduleLognormal Analysis with Arbitrary CensoringRegression ModelingRegression Model with Nonconstant ScaleRegression Model with Two Independent VariablesWeibull Probability Plot for Two Combined Failure ModesAnalysis of Recurrence Data on RepairsComparison of Two Samples of Repair DataAnalysis of Interval Age Recurrence DataAnalysis of Binomial DataThree-Parameter WeibullParametric Model for Recurrent Events DataParametric Model for Interval Recurrent Events Data -
Syntax
 Primary StatementsSecondary StatementsGraphical Enhancement StatementsPROC RELIABILITY StatementANALYZE StatementBY StatementCLASS StatementDISTRIBUTION StatementEFFECTPLOT StatementESTIMATE StatementFMODE StatementFREQ StatementINSET StatementLOGSCALE StatementLSMEANS StatementLSMESTIMATE StatementMAKE StatementMCFPLOT StatementMODEL StatementNENTER StatementNLOPTIONS StatementPROBPLOT StatementRELATIONPLOT StatementSLICE StatementSTORE StatementTEST StatementUNITID Statement
Primary StatementsSecondary StatementsGraphical Enhancement StatementsPROC RELIABILITY StatementANALYZE StatementBY StatementCLASS StatementDISTRIBUTION StatementEFFECTPLOT StatementESTIMATE StatementFMODE StatementFREQ StatementINSET StatementLOGSCALE StatementLSMEANS StatementLSMESTIMATE StatementMAKE StatementMCFPLOT StatementMODEL StatementNENTER StatementNLOPTIONS StatementPROBPLOT StatementRELATIONPLOT StatementSLICE StatementSTORE StatementTEST StatementUNITID Statement -
Details
 Abbreviations and NotationTypes of Lifetime DataProbability DistributionsProbability PlottingNonparametric Confidence Intervals for Cumulative Failure ProbabilitiesParameter Estimation and Confidence IntervalsRegression Model Statistics Computed for Each Observation for Lifetime DataRegression Model Statistics Computed for Each Observation for Recurrent Events DataRecurrence Data from Repairable SystemsODS Table NamesODS Graphics
Abbreviations and NotationTypes of Lifetime DataProbability DistributionsProbability PlottingNonparametric Confidence Intervals for Cumulative Failure ProbabilitiesParameter Estimation and Confidence IntervalsRegression Model Statistics Computed for Each Observation for Lifetime DataRegression Model Statistics Computed for Each Observation for Recurrent Events DataRecurrence Data from Repairable SystemsODS Table NamesODS Graphics - References
Nonparametric Confidence Intervals for Cumulative Failure Probabilities
The method used in the RELIABILITY procedure for computation of approximate pointwise and simultaneous confidence intervals for cumulative failure probabilities relies on the Kaplan-Meier estimator of the cumulative distribution function of failure time and approximate standard deviation of the Kaplan-Meier estimator. For the case of arbitrarily censored data, the Turnbull algorithm, discussed previously, provides an extension of the Kaplan-Meier estimator.
For multiply censored data, the Kaplan-Meier estimator of the cumulative distribution function at failure time 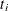 is
is 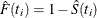 , where
, where
![\[ \hat{S}(t_ i) = \prod _{j=1}^{i}( 1 - \hat{p}_ j ), \]](images/qcug_reliability0131.png)
![\[ \hat{p}_ i = \frac{d_ i}{n_ i}, \]](images/qcug_reliability0132.png)
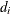 is the number of failures in the interval
is the number of failures in the interval 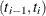 , and
, and 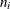 is the number of unfailed units at the beginning of the interval. This definition of the Kaplan-Meier estimator is equivalent
to the one previously given.
is the number of unfailed units at the beginning of the interval. This definition of the Kaplan-Meier estimator is equivalent
to the one previously given.
An estimator of the variance 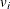 of the Kaplan-Meier estimator
of the Kaplan-Meier estimator 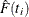 is given by
is given by
![\[ \hat{v}_ i = [\hat{S}(t_ i)]^2 \sum _{j=1}^ i\frac{\hat{p}_ j}{n_ j(1-\hat{p}_ j)} \]](images/qcug_reliability0138.png)
An estimator of the standard deviation of 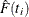 is
is 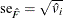 .
.
For arbitrarily censored data, the Kaplan-Meier estimator is replaced by the nonparametric maximum likelihood estimator computed
with the Turnbull algorithm, and the approximate variance of the estimator of 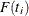 is computed from the inverse of the Fisher information matrix.
is computed from the inverse of the Fisher information matrix.
Pointwise Confidence Intervals
Approximate 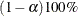 pointwise confidence intervals are computed as in Meeker and Escobar (1998, section 3.6) as
pointwise confidence intervals are computed as in Meeker and Escobar (1998, section 3.6) as
![\[ [ F_ L, F_ U ] = \left[ \frac{\hat{F}}{\hat{F} + ( 1-\hat{F})w}, \; \; \frac{\hat{F}}{\hat{F} + ( 1-\hat{F})/w} \right] \]](images/qcug_reliability0142.png)
where
![\[ w = \exp \left[\frac{z_{1-\alpha /2}\mbox{se}_{\hat{F}}}{(\hat{F}(1-\hat{F}))} \right] \]](images/qcug_reliability0143.png)
where 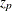 is the pth quantile of the standard normal distribution.
is the pth quantile of the standard normal distribution.
Simultaneous Confidence Intervals
Approximate 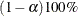 simultaneous confidence bands valid over the lifetime interval
simultaneous confidence bands valid over the lifetime interval 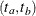 are computed as the "Equal Precision" case of Nair (1984) and Meeker and Escobar (1998, section 3.8)
are computed as the "Equal Precision" case of Nair (1984) and Meeker and Escobar (1998, section 3.8)
![\[ [ F_ L, F_ U ] = \left[ \frac{\hat{F}}{\hat{F} + ( 1-\hat{F})w}, \; \; \frac{\hat{F}}{\hat{F} + ( 1-\hat{F})/w} \right] \]](images/qcug_reliability0142.png)
where
![\[ w = \exp \left[\frac{e_{a,b,1-\alpha /2}\mbox{se}_{\hat{F}}}{(\hat{F}(1-\hat{F}))}\right] \]](images/qcug_reliability0146.png)
where the factor 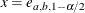 is the solution of
is the solution of
![\[ x\exp (-x^2/2)\log \left[\frac{(1-a)b}{(1-b)a}\right]/\sqrt {8\pi } = \alpha /2 \]](images/qcug_reliability0148.png)
The time interval 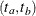 over which the bands are valid depends in a complicated way on the constants a and b defined in Nair (1984),
over which the bands are valid depends in a complicated way on the constants a and b defined in Nair (1984), 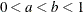 . a and b are chosen by default, so that the confidence bands are valid between the lowest and highest times corresponding to failures
in the case of multiply censored data, or, to the lowest and highest intervals for which probabilities are computed for arbitrarily
censored data. You can optionally specify a and b directly with the NPINTERVALS=SIMULTANEOUS(a,b) option in the PROBPLOT statement.
. a and b are chosen by default, so that the confidence bands are valid between the lowest and highest times corresponding to failures
in the case of multiply censored data, or, to the lowest and highest intervals for which probabilities are computed for arbitrarily
censored data. You can optionally specify a and b directly with the NPINTERVALS=SIMULTANEOUS(a,b) option in the PROBPLOT statement.