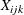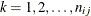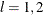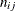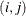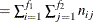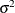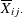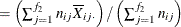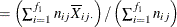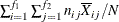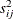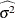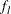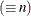XCHART Statement: ANOM Procedure

Constructing ANOM Charts for Two-Way Layouts

This section provides the computational details for constructing an ANOM chart for the lth factor in an experiment involving two factors (l = 1 or 2). It is assumed that there is no interaction effect. See Example 4.5 for an illustration.

The following notation is used in this section:

$X_{ijk}$

kth response at the ith level of factor 1 and the jth level of factor 2, where $k=1,2,\ldots ,n_{ij}$

$f_{l}$

Number of groups (levels) for the lth factor, $l=1,2$

$n_{ij}$

Number of replicates in cell $(i,j)$

N

Total sample size $= \sum _{i=1}^{f_1} \sum _{j=1}^{f_2} n_{ij}$

$\sigma ^2$

Variance of a response

$\overline{X}_{ij\cdot }$

Average response in cell $(i,j)$

$\overline{X}_{i\cdot \cdot }$

Average response for ith level of factor 1 $= \left( \sum _{j=1}^{f_2} n_{ij} \overline{X}_{ij\cdot } \right) / \left( \sum _{j=1}^{f_2} n_{ij} \right)$

$\overline{X}_{\cdot j\cdot }$

Average response for jth level of factor 2 $= \left( \sum _{i=1}^{f_1} n_{ij} \overline{X}_{ij\cdot } \right) / \left( \sum _{i=1}^{f_1} n_{ij} \right)$

$\overline{\overline{X}}$

$\sum _{i=1}^{f_1} \sum _{j=1}^{f_2} n_{ij} \overline{X}_{ij} / N$

$s_{ij}^{2}$

Sample variance of the responses for the ith level of factor 1 and the jth level of factor 2

$ \widehat{\sigma ^2}$

Mean square error (MSE) in the two-way analysis of variance

$\nu $

Degrees of freedom associated with the mean square error in the two-way analysis of variance

$\alpha $

Significance level

$h(\alpha ; f_ l, n, \nu )$

Critical value for analysis of means in a one-way layout for $f_ l$ groups (treatment levels) when the sample sizes for each level are constant $(\equiv n)$ and $\nu $ is the degrees of freedom associated with the mean square error; see the section Constructing ANOM Charts for Means.

Plotted Points

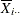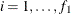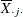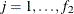The points on the ANOM chart for factor 1 represent $\overline{X}_{i\cdot \cdot }$, $i=1,\ldots ,f_1$ and the points on the ANOM chart for factor 2 represent $\overline{X}_{\cdot j\cdot }$, $j=1,\ldots ,f_2$.

Central Line

The central line on the ANOM chart for the lth factor is the overall weighted average 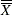$\overline{\overline{X}}$. Some authors use the notation 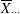$\overline{X}_{\cdot \cdot \cdot }$ for this average.

Decision Limits

It is assumed that

\[ X_{ijk} = \mu + \alpha _{i} + \beta _{j} + \epsilon _{ijk} \]

where the quantities 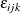$\epsilon _{ijk}$ are independent and at least approximately normally distributed with

\[ \epsilon _{ijk} \sim N( 0, \sigma ^2 ) \; \; \; \; \; \]

The correct decision limits for a given factor in a two-way layout are not computed by default when the lth factor is specified as the group-variable in the XCHART statement, since the mean square error and degrees of freedom are not adjusted for the two-way structure of the data. Consequently, 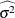$\widehat{\sigma ^2}$ and $\nu $ must be precomputed and provided to the ANOM procedure, as illustrated in Example 4.5.

In the case of a two-way layout with equal group sizes (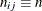$n_{ij} \equiv n$), the appropriate decision limits are:

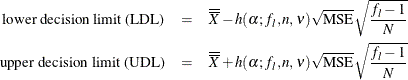
\begin{eqnarray*} \mbox{lower decision limit (LDL)} & = & \overline{\overline{X}} - h(\alpha ; f_ l, n, \nu ) \sqrt {\mbox{MSE}} \sqrt { \frac{f_{l}-1}{N}} \\ \mbox{upper decision limit (UDL)} & = & \overline{\overline{X}} + h(\alpha ; f_ l, n, \nu ) \sqrt {\mbox{MSE}} \sqrt {\frac{f_{l}-1}{N}} \end{eqnarray*}

where the mean square error (MSE) is computed as in the ANOVA or GLM procedure:

\[ \mbox{MSE} = \widehat{\sigma ^2} = \frac{1}{f_{1}f_{2}} \sum _{i=1}^{f_{1}} \sum _{j=1}^{f_{2}} s_{ij}^2 \]

and the degrees of freedom for error is 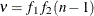$\nu = f_{1}f_{2}(n-1)$. For details concerning the function 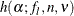$h(\alpha ; f_ l, n, \nu )$, see Nelson (1982a, 1993).

You can provide the appropriate values of MSE and $\nu $ by

  • specifying 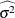$\widehat{\sigma ^2}$ with the MSE= option or with the variable _MSE_ in a LIMITS= data set

  • specifying $\nu $ with the DFE= option or with the variable _DFE_ in a LIMITS= data set

In addition you can:

  • Specify $\alpha $ with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set. By default,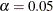 $\alpha = 0.05$.

  • Specify a constant nominal sample size 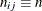$n_{ij} \equiv n$ for the decision limits in the balanced case with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set.

  • Specify 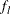$f_{l}$ with the LIMITK= option or with the variable _LIMITK_ in a LIMITS= data set.

  • Specify 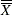$\overline{\overline{X}}$ with the MEAN= option or with the variable _MEAN_ in a LIMITS= data set.