The NLPC Nonlinear Optimization Solver: Optimization Algorithms :: SAS/OR(R) 9.22 User's Guide: Mathematical Programming

The NLPC Nonlinear Optimization Solver

Optimization Algorithms

There are four optimization algorithms available in the NLPC solver. A particular algorithm can be selected by using the TECH= option in the SOLVE statement.

Table 12.2 Algorithmic Options for the NLPC Solver
Algorithm	TECH=
Newton-type method with line search	NEWTYP
Trust region method	TRUREG
Conjugate gradient method	CONGRA
Quasi-Newton method (experimental)	QUANEW

Different optimization techniques require different derivatives, and computational efficiency can be improved depending on the kind of derivatives needed. Table 12.3 summarizes, for each optimization technique, which derivatives are needed (FOD: first-order derivatives; SOD: second-order derivatives) and what types of constraints (UNC: unconstrained; BC: bound constraints; LIC: linear constraints; NLC: nonlinear constraints) are supported.

Table 12.3 Types of Derivatives Required and Constraints Supported by Algorithm
	Derivatives Needed		Constraints Supported
	FOD	SOD	UNC	BC	LIC	NLC
TRUREG	x	x	x	x	x	-
NEWTYP	x	x	x	x	x	-
CONGRA	x	-	x	x	x	-
QUANEW	x	-	x	x	x	x

Choosing an Optimization Algorithm

Several factors play a role in choosing an optimization technique for a particular problem. First, the structure of the problem has to be considered: Is it unconstrained, bound constrained, or linearly constrained? The NLPC solver automatically identifies the structure and chooses an appropriate variant of the algorithm for the problem.

Next, it is important to consider the type of derivatives of the objective function and the constraints that are needed, and whether these are analytically tractable or not. This section provides some guidelines for making the choice. For an optimization problem, computing the gradient takes more computer time than computing the function value, and computing the Hessian matrix sometimes takes much more computer time and memory than computing the gradient, especially when there are many decision variables. Optimization techniques that do not use the Hessian usually require more iterations than techniques that do use the Hessian. The former tend to be slower and less reliable. However, the techniques that use the Hessian can be prohibitively slow for larger problems.

The following guidelines can be used in choosing an algorithm for a particular problem.

Without nonlinear constraints:
- Smaller Problems: TRUREG or NEWTYP
  if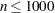 $\text{[math]}$ and the Hessian matrix is not expensive to compute. Sometimes NEWTYP can be faster than TRUREG, but TRUREG is generally more stable.
- Larger Problems: CONGRA
  if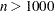 $\text{[math]}$ , the objective function and the gradient can be computed much more quickly than the Hessian, and too much memory is needed to store the Hessian. CONGRA in general needs more iterations than NEWTYP or TRUREG, but each iteration tends to be much faster. Since CONGRA needs less memory, many larger problems can be solved more efficiently by CONGRA.
With nonlinear constraints:
- QUANEW (experimental)
  QUANEW is the optimization method in the NLPC solver that solves problems with nonlinear constraints.

Trust Region Method (TRUREG)

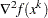The TRUREG method uses the gradient $\text{[math]}$ and the Hessian matrix $\text{[math]}$ , and it thus requires that the objective function 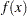$\text{[math]}$ have continuous first- and second-order partial derivatives inside the feasible region.

The trust region method iteratively optimizes a quadratic approximation to the nonlinear objective function within a hyperelliptic trust region with radius $\text{[math]}$ that constrains the step length corresponding to the quality of the quadratic approximation. The trust region method is implemented using the techniques described in Dennis, Gay, and Welsch (1981), Gay (1983), and Moré and Sorensen (1983).

The trust region method performs well for small to medium-sized problems and does not require many function, gradient, and Hessian calls. If the evaluation of the Hessian matrix is computationally expensive in larger problems, the conjugate gradient algorithm might be more appropriate.

Newton-Type Method with Line Search (NEWTYP)

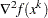The NEWTYP technique uses the gradient $\text{[math]}$ and the Hessian matrix $\text{[math]}$ , and it thus requires that the objective function have continuous first- and second-order partial derivatives inside the feasible region. If second-order partial derivatives are computed efficiently and precisely, the NEWTYP method can perform well for medium to large problems.

This algorithm uses a pure Newton step when the Hessian is positive definite and when the Newton step reduces the value of the objective function successfully. Otherwise, a combination of ridging and line search is done to compute successful steps. If the Hessian is not positive definite, a multiple of the identity matrix is added to the Hessian matrix to make it positive definite (Eskow and Schnabel 1991).

In each iteration, a line search is done along the search direction to find an approximate optimum of the objective function. The line-search method uses quadratic interpolation and cubic extrapolation.

Conjugate Gradient Method (CONGRA)

Second-order derivatives are not used by CONGRA. The CONGRA algorithm can be expensive in function and gradient calls but needs only 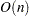$\text{[math]}$ memory for unconstrained optimization. In general, many iterations are needed to obtain a precise solution by using CONGRA, but each iteration is computationally inexpensive. The update formula for generating the conjugate directions uses the automatic restart update method of Powell (1977) and Beale (1972).

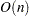The CONGRA method should be used for optimization problems with large $\text{[math]}$ . For the unconstrained or bound constrained case, CONGRA needs only $\text{[math]}$ bytes of working memory, whereas all other optimization methods require $\text{[math]}$ bytes of working memory. During $\text{[math]}$ successive iterations, uninterrupted by restarts or changes in the working set, the conjugate gradient algorithm computes a cycle of $\text{[math]}$ conjugate search directions. In each iteration, a line search is done along the search direction to find an approximate optimum of the objective function value. The line-search method uses quadratic interpolation and cubic extrapolation to obtain a step length $\text{[math]}$ satisfying the Goldstein conditions (Fletcher; 1987). Only one of the Goldstein conditions needs to be satisfied if the feasible region defines an upper limit for the step length.

Quasi-Newton Method (QUANEW) (Experimental)

The quasi-Newton method uses the gradient to approximate the Hessian. It works well for medium to moderately large optimization problems where the objective function and the gradient are much faster to compute than the Hessian, but in general it requires more iterations than the TRUREG and NEWTYP techniques, which compute the exact Hessian.

The specific algorithms implemented in the QUANEW technique depend on whether or not there are nonlinear constraints.

Unconstrained or Linearly Constrained Problems

If there are no nonlinear constraints, QUANEW updates the Cholesky factor of the approximate Hessian. In each iteration, a line search is done along the search direction to find an approximate optimum. The line-search method uses quadratic interpolation and cubic extrapolation to obtain a step length satisfying the Goldstein conditions.

Nonlinearly Constrained Problems

The algorithm implemented in the quasi-Newton method is an efficient modification of Powell’s (1978, 1982) Variable Metric Constrained WatchDog (VMCWD) algorithm. A similar but older algorithm (VF02AD) is part of the Harwell library. Both VMCWD and VF02AD use Fletcher’s VE02AD algorithm (part of the Harwell library) for strictly convex quadratic programming. The implementation in the NLPC solver uses a quadratic programming algorithm that updates the approximation of the Cholesky factor when the active set changes. The QUANEW method is not a feasible-point algorithm, and the value of the objective function might not decrease (minimization) or increase (maximization) monotonically. Instead, the algorithm tries to reduce the value of a merit function, a linear combination of the objective function and constraint violations.

Top of Page