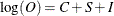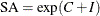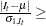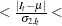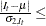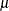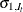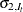The X13 Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryPROC X13 StatementADJUST StatementARIMA StatementAUTOMDL StatementBY StatementCHECK StatementESTIMATE StatementEVENT StatementFORECAST StatementID StatementIDENTIFY StatementINPUT StatementOUTLIER StatementOUTPUT StatementPICKMDL StatementREGRESSION StatementSEATSDECOMP StatementTABLES StatementTRANSFORM StatementUSERDEFINED StatementVAR StatementX11 Statement
Functional SummaryPROC X13 StatementADJUST StatementARIMA StatementAUTOMDL StatementBY StatementCHECK StatementESTIMATE StatementEVENT StatementFORECAST StatementID StatementIDENTIFY StatementINPUT StatementOUTLIER StatementOUTPUT StatementPICKMDL StatementREGRESSION StatementSEATSDECOMP StatementTABLES StatementTRANSFORM StatementUSERDEFINED StatementVAR StatementX11 Statement -
Details
 Data RequirementsMissing ValuesSAS Predefined EventsUser-Defined Regression VariablesCombined Test for the Presence of Identifiable SeasonalityComputationsPICKMDL Model SelectionSEATS DecompositionDisplayed Output, ODS Table Names, and OUTPUT Tablename KeywordsTable D 8.BUsing Auxiliary Variables to Subset Output Data SetsODS GraphicsOUT= Data SetSEATSDECOMP OUT= Data SetSpecial Data Sets
Data RequirementsMissing ValuesSAS Predefined EventsUser-Defined Regression VariablesCombined Test for the Presence of Identifiable SeasonalityComputationsPICKMDL Model SelectionSEATS DecompositionDisplayed Output, ODS Table Names, and OUTPUT Tablename KeywordsTable D 8.BUsing Auxiliary Variables to Subset Output Data SetsODS GraphicsOUT= Data SetSEATSDECOMP OUT= Data SetSpecial Data Sets -
Examples
 ARIMA Model IdentificationModel EstimationSeasonal AdjustmentRegARIMA Automatic Model SelectionAutomatic Outlier DetectionUser-Defined RegressorsMDLINFOIN= and MDLINFOOUT= Data SetsSetting Regression ParametersCreating an MDLINFO= Data Set for Use with the PICKMDL StatementIllustration of ODS GraphicsAUXDATA= Data Set
ARIMA Model IdentificationModel EstimationSeasonal AdjustmentRegARIMA Automatic Model SelectionAutomatic Outlier DetectionUser-Defined RegressorsMDLINFOIN= and MDLINFOOUT= Data SetsSetting Regression ParametersCreating an MDLINFO= Data Set for Use with the PICKMDL StatementIllustration of ODS GraphicsAUXDATA= Data Set - References
X11 Statement
-
X11 options;
The X11 statement is an optional statement for invoking seasonal adjustment by an enhanced version of the methodology of the US Census Bureau X-11 and X-11Q programs. You can control the type of seasonal adjustment decomposition calculated with the MODE= option. The output includes the final tables and diagnostics for the X-11 seasonal adjustment method listed in Table 45.7. Tables B7, B13, B17, B20, C1, E1, E2, E3, C20, D1, and D7 are not displayed by default; however, you can display these tables by requesting them in the TABLES statement .
Table 45.7: Tables Related to X11 Seasonal Adjustment
|
Table Name |
Description |
|
B1 |
Original series, adjusted for prior effects and forecast extended |
|
B7 |
Preliminary trend-cycle, B iteration |
|
B13 |
Irregular component, B iteration |
|
B17 |
Preliminary weights for the irregular component |
|
B20 |
Extreme values, B iteration |
|
C1 |
Original series modified for outliers, trading day, and prior factors, C iteration |
|
C17 |
Final weights for the irregular component |
|
C20 |
Final extreme value adjustment factors |
|
D1 |
Modified original data, D iteration |
|
D7 |
Preliminary trend cycle, D iteration |
|
D8 |
Final unmodified SI ratios (differences) |
|
D8A |
F tests for stable and moving seasonality, D8 |
|
D8B |
Final unmodified SI ratios, with labels for outliers and extreme values |
|
D9 |
Final replacement values for extreme SI ratios (differences), D iteration |
|
D9A |
Moving seasonality ratios for each period |
|
SeasonalFilter |
Seasonal filter statistics for Table D10 |
|
D10 |
Final seasonal factors |
|
D10B |
Seasonal factors, adjusted for user-defined seasonal |
|
D10D |
Final seasonal difference |
|
D11 |
Final seasonally adjusted series |
|
D11A |
Final seasonally adjusted series with forced yearly totals |
|
D11R |
Rounded final seasonally adjusted series (with forced yearly totals) |
|
TrendFilter |
Trend filter statistics for Table D12 |
|
D12 |
Final trend cycle |
|
D13 |
Final irregular component |
|
D16 |
Combined seasonal and trading day factors |
|
D16B |
Final adjustment differences |
|
D18 |
Combined calendar adjustment factors |
|
E1 |
Original data modified for extremes |
|
E2 |
Modified seasonally adjusted series |
|
E3 |
Modified irregular series |
|
E4 |
Ratio of yearly totals of original and seasonally adjusted series |
|
E5 |
Percent changes (differences) in original series |
|
E6 |
Percent changes (differences) in seasonally adjusted series |
|
E6A |
Percent changes (differences) in seasonally adjusted series with forced yearly totals (D11.A) |
|
E6R |
Percent changes (differences) in rounded seasonally adjusted series (D11.R) |
|
E7 |
Percent changes (differences) in final trend component series |
|
E8 |
Percent changes (differences) in original series adjusted for calendar factors (A18) |
|
E18 |
Final adjustment ratios (original series to seasonally adjusted series) |
|
F2A–F2I |
X11 diagnostic summary |
|
F3 |
Monitoring and quality assessment statistics |
|
F4 |
Day of the week trading day component factors |
|
G |
Spectral plots |
For more information about the X-11 seasonal adjustment diagnostics, see Shiskin, Young, and Musgrave (1967), Lothian and Morry (1978a), and Ladiray and Quenneville (2001).
You can specify the following options in the X11 statement:
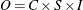
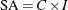
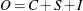
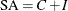
![$O = C \times [ S + I - 1 ]$](images/etsug_x130078.png)