The X11 Procedure
- Overview
-
Getting Started
-
Syntax
-
DetailsHistorical Development of X-11Implementation of the X-11 Seasonal Adjustment MethodComputational Details for Sliding Spans AnalysisData RequirementsMissing ValuesPrior Daily Weights and Trading-Day RegressionAdjustment for Prior FactorsThe YRAHEADOUT OptionEffect of Backcast and Forecast LengthDetails of Model SelectionOUT= Data SetThe OUTSPAN= Data SetOUTSTB= Data SetOUTTDR= Data SetPrinted OutputODS Table Names
-
Examples
- References
Effect of Backcast and Forecast Length
Based on a number of empirical studies (Dagum 1982a, 1982b, 1982c; Dagum and Laniel 1987), one year of forecasts minimize revisions when new data become available. Two and three years of forecasts show only small gains.
Backcasting improves seasonal adjustment but introduces permanent revisions at the beginning of the series and also at the end for series of length 8, 9, or 10 years. For series shorter than 7 years, the advantages of backcasting outweigh the disadvantages (Dagum 1988).
Other studies (Pierce 1980; Bobbit and Otto 1990; Buszuwski 1987) suggest "full forecasting"— that is, using enough forecasts to allow symmetric weights for the seasonal moving averages
for the most current data. For example, if a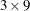 
seasonal moving average was specified for one or more months by using the MACURVES statement, five years of forecasts would
be required. This is because the seasonal moving averages are performed on calendar months separately, and the 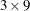is an 11-term centered moving average, requiring five observations before and after the current observation. Thus
macurves dec='3x9';
would require five additional December values to compute the seasonal moving average.