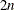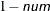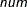The TIMESERIES Procedure

SPECTRA Statement

Subsections:

  • SPECTRA statistics < / options>;

You can use a SPECTRA statement to specify which statistics appear in the OUTSPECTRA= data set. The SPECTRA statement options are used in performing a spectral analysis on the variables listed in the VAR statement. These options affect values that are produced in the PROC TIMESERIES statement’s OUTSPECTRA= data set, and in the periodogram and spectral density estimate. Only one SPECTRA statement is allowed.

You can request the following univariate frequency domain statistics:

FREQ

frequency in radians from 0 to $\pi $

PERIOD

period or wavelength

COS

cosine transform

SIN

sine transform

P

periodogram

S

spectral density estimates

If you do not specify any frequency domain statistics, then the default is as follows: 

   spectra period p;

You can also specify the following options after a slash (/):

C=coefficient

specifies the scale coefficient for the kernel function. For more information, see the section Kernel Option Details.

E=exponent
EXP=exponent
EXPON=exponent

specifies the exponent for the kernel function. For more information, see the section Kernel Option Details.

ADJUSTMEAN=NO | YES
CENTER=NO | YES

specifies whether the series is to be adjusted by its mean prior to performing the Fourier decomposition. This adjustment sets the first periodogram ordinate to 0 rather than to $2 n$ times the squared mean. This option is commonly used when the periodograms are to be plotted to prevent a large first periodogram ordinate from distorting the scale of the plot.

NO

specifies that no adjustment of the series be performed.

YES

specifies that the series be transformed by subtracting its mean.

By default, ADJUSTMEAN=NO.

ALPHA=num

specifies the width of a window that is drawn around the spectral density estimate in a spectral density versus frequency plot. Based on approximations proposed by Brockwell and Davis (1991), periodogram ordinates fall within this window with a confidence level of $1-\Argument{num}$. The value $\Argument{num}$ must be between 0 and 1; the default is 0.05.

DOMAIN=domain

specifies how the smoothing function is interpreted. You can specify the following domain values:

FREQUENCY

smooths the periodogram ordinates.

TIME

applies the kernel as a filter to the time series autocovariance function.

By default DOMAIN=FREQUENCY, and smoothing is applied in the same manner as weights are applied when you specify the WEIGHTS= option.

kernel

specifies the smoothing function to use to calculate a spectral density estimate as the moving average of periodogram ordinates. The kernel function is an alternative smoothing method to using the WEIGHTS= option. You can specify the following kernel values:

PARZEN

Parzen kernel

BARTLETT

Bartlett kernel

TUKEY

Tukey-Hanning kernel

TRUNC | TRUNCAT

truncated kernel

QS | QUADR

quadratic spectral kernel

If neither a WEIGHTS= option nor a kernel function is specified, the spectral density estimate is identical to the unmodified periodogram.

WEIGHTS=numlist

specifies the relative weights to use to compute a spectral density estimate as the moving average smoothing of periodogram ordinates. If neither a WEIGHTS= option nor a kernel function is specified, the spectral density estimate is identical to the unmodified periodogram. The following SPECTRA statement uses the WEIGHTS= option to specify equal weighting for each of the three adjacent periodogram ordinates that are centered on each spectral density estimate: 

   spectra / weights 1 1 1;

For information about how the weights are applied, see the section Using Specification of Weight Constants.

Kernel Option Details

You can further parameterize each of the kernel functions with a kernel scale factor by using the C= and E= options. The default values of the kernel scale parameters, c and e, that are associated with each of the kernel functions together with their kernel scale factor values, M, for a series with 100 periodogram ordinates are listed in Table 39.2. The formula that is used to generate the table entries is 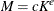$M=c{K}^{e}$, where K is the number of Fourier component frequencies.

Table 39.2: Default Kernel Scale Factor Parameters

Kernel

c

e

M

Bartlett

1/2

1/3

2.32

Parzen

1

1/5

2.51

Quadratic

1/2

1/5

1.26

Tukey-Hanning

2/3

1/5

1.67

Truncated

1/4

1/5

0.63


For example, to apply the truncated kernel by using default scale factor parameters in the frequency domain, you could use the following SPECTRA statement: 

   spectra / truncat;

For more information about the kernel function parameterization and the DOMAIN= option, see the section Using Kernel Specifications.