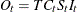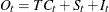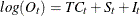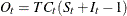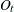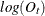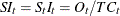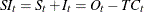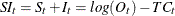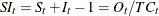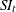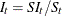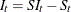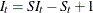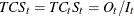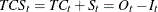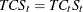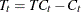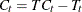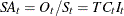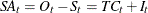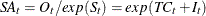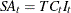The TIMESERIES Procedure

Seasonal Decomposition

Seasonal decomposition/analysis can be performed on the working series by specifying the OUTDECOMP= option, the PRINT=DECOMP option, or one of the PLOTS= options associated with decomposition in the PROC TIMESERIES statement. The DECOMP statement enables you to specify options related to decomposition. The TIMESERIES procedure uses classical decomposition. More complex seasonal decomposition/adjustment analysis can be performed by using the X11 or the X12 procedure of SAS/ETS.

The DECOMP statement MODE= option determines the mode of the seasonal adjustment decomposition to be performed. There are four modes: multiplicative (MODE=MULT), additive (MODE=ADD), pseudo-additive (MODE=PSEUDOADD), and log-additive (MODE=LOGADD) decomposition. The default is MODE=MULTORADD which specifies MODE=MULT for series that are strictly positive, MODE=PSEUDOADD for series that are nonnegative, and MODE=ADD for series that are not nonnegative.

When MODE=LOGADD is specified, the components are exponentiated to the original metric.

The DECOMP statement LAMBDA= option specifies the Hodrick-Prescott filter parameter (Hodrick and Prescott 1980). The default is LAMBDA=1600. The Hodrick-Prescott filter is used to decompose the trend-cycle component into the trend component and cycle component in an additive fashion. A smaller parameter assigns less significance to the cycle; that is, LAMBDA=0 implies no cycle component.

The notation and keywords associated with seasonal decomposition/adjustment analysis are defined in Table 39.3.

Table 39.3: Seasonal Adjustment Formulas

Component	Keyword	MODE= Option	Formula
original series	ORIGINAL	MULT	${ O_{t} = TC_{t}S_{t}I_{t} }$
		ADD	${ O_{t} = TC_{t}+S_{t}+I_{t} }$
		LOGADD	${ log(O_{t}) = TC_{t}+S_{t}+I_{t} }$
		PSEUDOADD	${ O_{t} = TC_{t}(S_{t}+I_{t}-1) }$
trend-cycle component	TCC	MULT	centered moving average of ${O_{t}}$
		ADD	centered moving average of ${O_{t}}$
		LOGADD	centered moving average of ${log(O_{t})}$
		PSEUDOADD	centered moving average of ${O_{t}}$
seasonal-irregular component	SIC	MULT	${ SI_{t} = S_{t}I_{t} = O_{t}/TC_{t} }$
		ADD	${ SI_{t} = S_{t}+I_{t} = O_{t}-TC_{t} }$
		LOGADD	${ SI_{t} = S_{t}+I_{t} = log(O_{t})-TC_{t} }$
		PSEUDOADD	${ SI_{t} = S_{t}+I_{t}-1 = O_{t}/TC_{t} }$
seasonal component	SC	MULT	seasonal Averages of ${SI_{t}}$
		ADD	seasonal Averages of ${SI_{t}}$
		LOGADD	seasonal Averages of ${SI_{t}}$
		PSEUDOADD	seasonal Averages of ${SI_{t}}$
irregular component	IC	MULT	${ I_{t} = SI_{t}/S_{t} }$
		ADD	${ I_{t} = SI_{t}-S_{t} }$
		LOGADD	${ I_{t} = SI_{t}-S_{t} }$
		PSEUDOADD	${ I_{t} = SI_{t}-S_{t} + 1 }$
trend-cycle-seasonal component	TCS	MULT	${ TCS_{t} = TC_{t}S_{t} = O_{t}/I_{t} }$
		ADD	${ TCS_{t} = TC_{t}+S_{t} = O_{t}-I_{t} }$
		LOGADD	${ TCS_{t} = TC_{t}+S_{t} = O_{t}-I_{t} }$
		PSEUDOADD	${ TCS_{t} = TC_{t}S_{t} }$
trend component	TC	MULT	${ T_{t} = TC_{t}-C_{t} }$
		ADD	${ T_{t} = TC_{t}-C_{t} }$
		LOGADD	${ T_{t} = TC_{t}-C_{t} }$
		PSEUDOADD	${ T_{t} = TC_{t}-C_{t} }$
cycle component	CC	MULT	${ C_{t} = TC_{t}-T_{t} }$
		ADD	${ C_{t} = TC_{t}-T_{t} }$
		LOGADD	${ C_{t} = TC_{t}-T_{t} }$
		PSEUDOADD	${ C_{t} = TC_{t}-T_{t} }$
seasonally adjusted series	SA	MULT	${ SA_{t} = O_{t}/S_{t} = TC_{t}I_{t} }$
		ADD	${ SA_{t} = O_{t}-S_{t} = TC_{t}+I_{t} }$
		LOGADD	${ SA_{t} = O_{t}/exp(S_{t}) = exp(TC_{t}+I_{t}) }$
		PSEUDOADD	${ SA_{t} = TC_{t}I_{t} }$

When ${s}$ is odd the trend-cycle component is computed from the ${s}$ -period centered moving average as follows:

$TC_{t} = \sum _{k=-{\lfloor s/2 \rfloor }}^{{\lfloor s/2 \rfloor }}{y_{t+k}/s}$

When ${s}$ is even the trend-cycle component is computed from the ${s}$ -period centered moving average as follows:

$TC_{t} = \sum _{k=-{s/2}}^{{s/2}-1}{(y_{t+k}+y_{t+1+k})/2s}$

The seasonal component is obtained by averaging the seasonal-irregular component for each season.

$S_{k+js} = \sum _{t = k \bmod s}\frac{SI_ t}{T/s}$

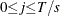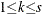where ${0 {\le } j {\le } T/s }$ and ${1 {\le } k {\le } s }$ . The seasonal components are normalized to sum to one (multiplicative) or zero (additive).