The SYSLIN Procedure
- Overview
-
Getting Started
 An Example ModelVariables in a System of EquationsUsing PROC SYSLINOLS EstimationTwo-Stage Least Squares EstimationLIML, K-Class, and MELO EstimationSUR, 3SLS, and FIML EstimationComputing Reduced Form EstimatesRestricting Parameter EstimatesTesting ParametersSaving Residuals and Predicted ValuesPlotting Residuals
An Example ModelVariables in a System of EquationsUsing PROC SYSLINOLS EstimationTwo-Stage Least Squares EstimationLIML, K-Class, and MELO EstimationSUR, 3SLS, and FIML EstimationComputing Reduced Form EstimatesRestricting Parameter EstimatesTesting ParametersSaving Residuals and Predicted ValuesPlotting Residuals -
Syntax

-
Details

-
Examples

- References
TEST Statement
-
TEST equation , …, equation / options;
The TEST statement performs F tests of linear hypotheses about the parameters in the preceding MODEL statement. Each equation specifies a linear hypothesis to be tested. If more than one equation is specified, the equations are separated by commas.
Variable names must correspond to regressors in the preceding MODEL statement, and each name represents the coefficient of the corresponding regressor. The keyword INTERCEPT is used to refer to the model intercept.
TEST statements can be given labels. The label is used in the printed output to distinguish different tests. Any number of TEST statements can be specified. Labels are specified as follows:
-
label : TEST …;
The following is an example of the use of TEST statement, which tests the hypothesis that the coefficients of X1 and X2 are the same:
proc syslin data=a;
model y = x1 x2;
test x1 = x2;
run;
The following statements perform F tests for the hypothesis that the coefficients of X1 and X2 are equal, for the hypothesis that the sum of the X1 and X2 coefficients is twice the intercept, and for the joint hypothesis.
proc syslin data=a;
model y = x1 x2;
x1eqx2: test x1 = x2;
sumeq2i: test x1 + x2 = 2 * intercept;
joint: test x1 = x2, x1 + x2 = 2 * intercept;
run;
The following are additional examples of TEST statements:
test x1 + x2 = 1; test x1 = x2 = x3 = 1; test 2 * x1 = x2 + x3, intercept + x4 = 0; test 2 * x1 - x2;
The TEST statement performs an F test for the joint hypotheses specified. The hypothesis is represented in matrix notation as follows:
![\[ \mb{L} {\beta }=\mb{c} \]](images/etsug_syslin0017.png)
The F test is computed as
![\[ \frac{(\mb{L} b-\mb{c} )' (\mb{L} (\mb{X'X} )^{-}\mb{L} ')^{-1} (\mb{L} b-\mb{c} )}{m\hat{{\sigma }}^{2}} \]](images/etsug_syslin0022.png)
where b is the estimate of 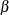 , m is the number of restrictions, and
, m is the number of restrictions, and 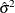 is the model mean squared error. See the section Computational Details for information about the matrix
is the model mean squared error. See the section Computational Details for information about the matrix 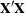 .
.
The test performed is exact only for ordinary least squares, given the OLS assumptions of the linear model. For other estimation methods, the F test is based on large sample theory and is only approximate in finite samples.
If RESTRICT or SRESTRICT statements are used, the tests computed by the TEST statement are conditional on the restrictions specified. The validity of the tests can be compromised if incorrect restrictions are imposed on the estimates.
The PRINT option can be specified in the TEST statement after a slash (/):