The SYSLIN Procedure

PROC SYSLIN performs OLS regression if you do not specify a method of estimation in the PROC SYSLIN statement. OLS does not use instruments, so the ENDOGENOUS and INSTRUMENTS statements can be omitted.

The following statements estimate the supply and demand model shown previously:

proc syslin data=in;
   demand: model q = p y s;
   supply: model q = p u;
run;

The PROC SYSLIN output for the demand equation is shown in Figure 36.1, and the output for the supply equation is shown in Figure 36.2.

For each MODEL statement, the output first shows the model label and dependent variable name and label. This is followed by an analysis-of-variance table for the model, which shows the model, error, and total mean squares, and an F test for the no-regression hypothesis. Next, the procedure prints the root mean squared error, dependent variable mean and coefficient of variation, and the 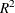and adjusted 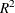statistics.

Finally, the table of parameter estimates shows the estimated regression coefficients, standard errors, and t tests. You would expect the price coefficient in a demand equation to be negative. However, note that the OLS estimate of the price coefficient P in the demand equation (0.1233) has a positive sign. This could be caused by simultaneous equation bias.