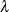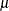The HPCOUNTREG Procedure

MODEL Statement

Subsections:

  • MODEL dependent-variable = regressors </ options>;

The MODEL statement specifies the dependent variable and independent regressor variables for the regression model. The dependent count variable should take only nonnegative integer values from the input data set. PROC HPCOUNTREG rounds any positive noninteger count value to the nearest integer. PROC HPCOUNTREG discards any observation that has a negative count.

Only one MODEL statement can be specified. You can specify the following options in the MODEL statement after a slash (/).

DIST=value

specifies a type of model to be analyzed. You can specify the following values:

POISSON | P

specifies the Poisson regression model.

CMPOISSON | C | CMP

specifies a Conway-Maxwell-Poisson regression model.

NEGBIN(P=1)

specifies the negative binomial regression model that uses a linear variance function.

NEGBIN(P=2) | NEGBIN

specifies the negative binomial regression model that uses a quadratic variance function.

ZIPOISSON | ZIP

specifies zero-inflated Poisson regression.

ZICMPOISSON | ZICMP

specifies a zero-inflated Conway-Maxwell-Poisson regression. The ZEROMODEL statement must be specified when this model type is specified.

ZINEGBIN | ZINB

specifies zero-inflated negative binomial regression.

You can also specify the DIST option in the HPCOUNTREG statement.

ERRORCOMP=FIXED | RANDOM

specifies a type of conditional panel model to be analyzed. You can specify the following model types:

FIXED

specifies a fixed-effect error component regression model.

RANDOM

specifies a random-effect error component regression model.

NOINT

suppresses the intercept parameter.

OFFSET=offset-variable

specifies a variable in the input data set to be used as an offset variable. The offset-variable is used to allow the observational units to vary across observations. For example, when the number of shipping accidents could be measured across different time periods or the number of students who participate in an activity could be reported across different class sizes, the observational units need to be adjusted to a common denominator by using the offset variable. The offset variable appears as a covariate in the model with its parameter restricted to 1. The offset variable cannot be the response variable, the zero-inflation offset variable (if any), or any of the explanatory variables. The "Model Fit Summary" table gives the name of the data set variable that is used as the offset variable; it is labeled "Offset."

PARAMETER=MU | LAMBDA

specifies the parameterization for the Conway-Maxwell-Poisson model. The following parameterizations are supported:

LAMBDA

estimates the original Conway-Maxwell-Poisson model (Shmueli et al. 2005).

MU

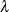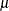reparameterizes $\lambda $ as documented by Guikema and Coffelt (2008), where $\mu =\lambda ^{1/{\nu }} $ and the integral part of $\mu $ represents the mode, which can be considered a measure of central tendency (mean).

By default, PARAMETER=MU.

Printing Options

You can specify the following options in either the PROC HPCOUNTREG statement or the MODEL statement:

CORRB

prints the correlation matrix of the parameter estimates.

COVB

prints the covariance matrix of the parameter estimates.

NOPRINT

suppresses all printed output.

PRINTALL

requests all printing options.