The HPCOUNTREG Procedure

Getting Started: HPCOUNTREG Procedure

Except for its ability to operate in the high-performance distributed environment, the HPCOUNTREG procedure is similar in use to other regression model procedures in the SAS System. For example, the following statements are used to estimate a Poisson regression model:

   proc hpcountreg data=one ;
      model y = x / dist=poisson ;
   run;

The response variable y is numeric and has nonnegative integer values.

This section illustrates two simple examples that use PROC HPCOUNTREG. The data are taken from Long (1997). This study examines how factors such as gender (fem), marital status (mar), number of young children (kid5), prestige of the graduate program (phd), and number of articles published by a scientist’s mentor (ment) affect the number of articles (art) published by the scientist.

The first 10 observations are shown in Figure 20.1.

Figure 20.1: Article Count Data

Obs	art	mar	kid5	phd	ment
1	3	1	2	1.38000	8.0000
2	0	0	0	4.29000	7.0000
3	4	0	0	3.85000	47.0000
4	1	1	1	3.59000	19.0000
5	1	1	0	1.81000	0.0000
6	1	1	1	3.59000	6.0000
7	0	1	1	2.12000	10.0000
8	0	1	0	4.29000	2.0000
9	3	1	2	2.58000	2.0000
10	3	1	1	1.80000	4.0000

The following SAS statements estimate the Poisson regression model. The model is executed in the distributed computing environment with two threads and four nodes.


/*-- Poisson Regression --*/
proc hpcountreg data=long97data;
   model art = fem mar kid5 phd ment / dist=poisson method=quanew;
   performance nthreads=2 nodes=4 details;
run;

The "Model Fit Summary" table that is shown in Figure 20.2 lists several details about the model. By default, the HPCOUNTREG procedure uses the Newton-Raphson optimization technique. The maximum log-likelihood value is shown, in addition to two information measures—Akaike’s information criterion (AIC) and Schwarz’s Bayesian information criterion (SBC)—which can be used to compare competing Poisson models. Smaller values of these criteria indicate better models.

Figure 20.2: Estimation Summary Table for a Poisson Regression

The HPCOUNTREG Procedure

Model Fit Summary
Dependent Variable	art
Number of Observations	915
Data Set	WORK.LONG97DATA
Model	Poisson
Log Likelihood	-1651
Maximum Absolute Gradient	0.0002080
Number of Iterations	13
Optimization Method	Quasi-Newton
AIC	3314
SBC	3343

Figure 20.3 shows the parameter estimates of the model and their standard errors. All covariates are significant predictors of the number of articles, except for the prestige of the program (phd), which has a p-value of 0.6271.

Figure 20.3: Parameter Estimates of Poisson Regression

Parameter Estimates
Parameter	DF	Estimate	Standard Error	t Value	Pr > \|t\|
Intercept	1	0.3046	0.1030	2.96	0.0031
fem	1	-0.2246	0.05461	-4.11	<.0001
mar	1	0.1552	0.06137	2.53	0.0114
kid5	1	-0.1849	0.04013	-4.61	<.0001
phd	1	0.01282	0.02640	0.49	0.6271
ment	1	0.02554	0.002006	12.73	<.0001

To allow for variance greater than the mean, you can fit the negative binomial model instead of the Poisson model by specifying the DIST=NEGBIN option, as shown in the following statements. Whereas the Poisson model requires that the conditional mean and conditional variance be equal, the negative binomial model allows for overdispersion, in which the conditional variance can exceed the conditional mean.

/*-- Negative Binomial Regression --*/
proc hpcountreg data=long97data;
   model art = fem mar kid5 phd ment / dist=negbin(p=2) method=quanew;
   performance nthreads=2 nodes=4 details;
run;

Figure 20.4 shows the fit summary and Figure 20.5 shows the parameter estimates.

Figure 20.4: Estimation Summary Table for a Negative Binomial Regression

The HPCOUNTREG Procedure

Model Fit Summary
Dependent Variable	art
Number of Observations	915
Data Set	WORK.LONG97DATA
Model	NegBin
Log Likelihood	-1561
Maximum Absolute Gradient	0.0000666
Number of Iterations	16
Optimization Method	Quasi-Newton
AIC	3136
SBC	3170

Figure 20.5: Parameter Estimates of Negative Binomial Regression

Parameter Estimates
Parameter	DF	Estimate	Standard Error	t Value	Pr > \|t\|
Intercept	1	0.2561	0.1386	1.85	0.0645
fem	1	-0.2164	0.07267	-2.98	0.0029
mar	1	0.1505	0.08211	1.83	0.0668
kid5	1	-0.1764	0.05306	-3.32	0.0009
phd	1	0.01527	0.03604	0.42	0.6718
ment	1	0.02908	0.003470	8.38	<.0001
_Alpha	1	0.4416	0.05297	8.34	<.0001

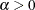The parameter estimate for _Alpha of 0.4416 is an estimate of the dispersion parameter in the negative binomial distribution. A t test for the hypothesis $H_0: \alpha =0$ is provided. It is highly significant, indicating overdispersion ( $p<0.0001$ ).

The null hypothesis $H_0: \alpha =0$ can be also tested against the alternative $\alpha > 0$ by using the likelihood ratio test, as described by Cameron and Trivedi (1998, pp. 45, 77–78). The likelihood ratio test statistic is equal to $-2(\mathcal{L}_{P}-\mathcal{L}_{NB})=-2(-1651+1561)=180$ , which is highly significant, providing strong evidence of overdispersion.