The HPCOUNTREG Procedure

DISPMODEL Statement

  • DISPMODEL dependent-variable 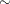$\sim $ <dispersion-related-regressors>;

The DISPMODEL statement specifies the dispersion-related-regressors that are used to model dispersion. This statement is ignored unless you specify DIST=CMPOISSON in the MODEL statement. The dependent-variable in the DISPMODEL statement must be the same as the dependent-variable in the MODEL statement.

The dependent-variable that appears in the DISPMODEL statement is directly used to model dispersion. Each of the q variables to the right of the tilde (~) has a parameter to be estimated in the regression. For example, let 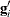$\mathbf{g}_{i}’$ be the ith observation’s 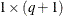$1 \times (q+1)$ vector of values of the q dispersion explanatory variables (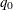$q_0$ is set to 1 for the intercept term). Then the dispersion is a function of 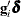$\mathbf{g}_{i}’\bdelta $, where 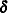$\bdelta $ is the 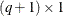$(q+1) \times 1$ vector of parameters to be estimated, the dispersion model intercept is 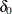$\delta _0$, and the coefficients for the q dispersion covariates are 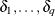$\delta _1, \ldots , \delta _ q$. If you specify DISP=CMPOISSON in the MODEL statement but do not include a DISPMODEL statement, then only the intercept term 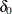$\delta _0$ is estimated. The “Parameter Estimates” table in the displayed output shows the estimates for the dispersion intercept and dispersion explanatory variables; they are labeled with the prefix "Disp_". For example, the dispersion intercept is labeled "Disp_Intercept". If you specify Age (a variable in your data set) as a dispersion explanatory variable, then the “Parameter Estimates” table labels the corresponding parameter estimate "Disp_Age". The following statements fit a Conway-Maxwell-Poisson model by using the regressors SEX, ILLNESS, and INCOME and by using AGE as a dispersion-related regressor: 

   proc hpcountreg data=docvisit;
      model doctorvisits=sex illness income / dist=cmpoisson;
      dispmodel doctorvisits ~ age;
   run;