The ENTROPY Procedure(Experimental)
- Overview
-
Getting Started

-
Syntax

-
Details
 Generalized Maximum EntropyGeneralized Cross EntropyMoment Generalized Maximum EntropyMaximum Entropy-Based Seemingly Unrelated RegressionGeneralized Maximum Entropy for Multinomial Discrete Choice ModelsCensored or Truncated Dependent VariablesInformation MeasuresParameter Covariance For GCEParameter Covariance For GCE-MStatistical TestsMissing ValuesInput Data SetsOutput Data SetsODS Table NamesODS Graphics
Generalized Maximum EntropyGeneralized Cross EntropyMoment Generalized Maximum EntropyMaximum Entropy-Based Seemingly Unrelated RegressionGeneralized Maximum Entropy for Multinomial Discrete Choice ModelsCensored or Truncated Dependent VariablesInformation MeasuresParameter Covariance For GCEParameter Covariance For GCE-MStatistical TestsMissing ValuesInput Data SetsOutput Data SetsODS Table NamesODS Graphics -
Examples

- References
Generalized Maximum Entropy
Reparameterization of the errors in a regression equation is the process of specifying a support for the errors, observation
by observation. If a two-point support is used, the error for the tth observation is reparameterized by setting 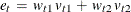 , where
, where 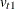 and
and 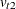 are the upper and lower bounds for the tth error
are the upper and lower bounds for the tth error 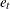 , and
, and 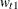 and
and 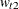 represent the weight associated with the point
represent the weight associated with the point 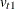 and
and 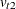 . The error distribution is usually chosen to be symmetric, centered around zero, and the same across observations so that
. The error distribution is usually chosen to be symmetric, centered around zero, and the same across observations so that
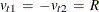 , where R is the support value chosen for the problem (Golan, Judge, and Miller 1996).
, where R is the support value chosen for the problem (Golan, Judge, and Miller 1996).
The generalized maximum entropy (GME) formulation was proposed for the ill-posed or underdetermined case where there is insufficient
data to estimate the model with traditional methods. 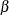 is reparameterized by defining a support for
is reparameterized by defining a support for 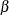 (and a set of weights in the cross entropy case), which defines a prior distribution for
(and a set of weights in the cross entropy case), which defines a prior distribution for 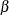 .
.
In the simplest case, each 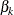 is reparameterized as
is reparameterized as 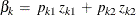 , where
, where 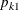 and
and 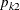 represent the probabilities ranging from [0,1] for each
represent the probabilities ranging from [0,1] for each 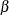 , and
, and 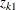 and
and 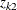 represent the lower and upper bounds placed on
represent the lower and upper bounds placed on 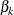 . The support points,
. The support points, 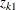 and
and 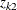 , are usually distributed symmetrically around the most likely value for
, are usually distributed symmetrically around the most likely value for 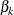 based on some prior knowledge.
based on some prior knowledge.
With these reparameterizations, the GME estimation problem is
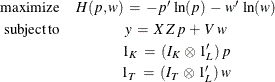
where y denotes the column vector of length T of the dependent variable; 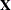 denotes the
denotes the 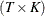 matrix of observations of the independent variables; p denotes the LK column vector of weights associated with the points in Z; w denotes the LT column vector of weights associated with the points in V;
matrix of observations of the independent variables; p denotes the LK column vector of weights associated with the points in Z; w denotes the LT column vector of weights associated with the points in V; 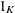 ,
, 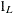 , and
, and 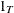 are K-, L-, and T-dimensional column vectors, respectively, of ones; and
are K-, L-, and T-dimensional column vectors, respectively, of ones; and 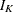 and
and 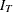 are
are 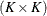 and
and 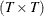 dimensional identity matrices.
dimensional identity matrices.
These equations can be rewritten using set notation as follows:
![\[ \mr{maximize} \; \; \; H(p,w) \: = \: - \, \sum _{l=1}^{L} \, \sum _{k=1}^{K} \: p_{kl} \, \ln (p_{kl}) \: - \: \sum _{l=1}^{L} \, \sum _{t=1}^{T} \: w_{tl} \, \ln (w_{tl}) \]](images/etsug_entropy0063.png)
![\[ \mr{subject\, to} \; \; \; y_ t \: = \: \sum _{l=1}^{L} \left[ \, \sum _{k=1}^{K} \: \left( \, X_{kt} \, Z_{kl} \, p_{kl} \right) \: + \: V_{tl} \, w_{tl} \right] \]](images/etsug_entropy0064.png)
![\[ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \sum _{l=1}^{L} \: p_{kl}\: = \: 1 \; \; \mr{and} \; \; \sum _{l=1}^{L} \: w_{tl} \: = \: 1 \]](images/etsug_entropy0065.png)
The subscript l denotes the support point (l=1, 2, ..., L), k denotes the parameter (k=1, 2, ..., K), and t denotes the observation (t=1, 2, ..., T).
The GME objective is strictly concave; therefore, a unique solution exists. The optimal estimated probabilities, p and w, and the prior supports, Z and V, can be used to form the point estimates of the unknown parameters, 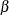 , and the unknown errors, e.
, and the unknown errors, e.