Usage Note 57975: Understanding splines in the EFFECT statement
 |  |  |
A spline is a piecewise polynomial function in which the individual polynomials are of the same degree and which connect smoothly at join points whose abscissa values, referred to as knots, are pre-defined. You can use splines to obtain a more flexible fit to the data than can be obtained with a regular linear regression model.
Spline effects can be defined using the EFFECT statement that is available in several procedures. See the discussion of splines in the documentation of the EFFECT statement in the Shared Concepts and Topics chapter of the SAS/STAT® User's Guide. The following example illustrates fitting a model containing a spline effect in PROC GLIMMIX. It discusses the spline basis output, the interpretation of the output, how to use the spline model to make predictions, and how to use the LSMEANS and ESTIMATE statements to compute quantities of interest.
Example
Data were collected from an experiment about gasoline engine exhaust emissions. Nitrogen oxide (NOx) emissions from a single-cylinder engine were measured for various combinations of fuel, compression ratio (CpRatio), and equivalence ratio (EqRatio) which is the ratio of the actual air-fuel ratio to the ideal air-fuel ratio. These statements display a subset of the data for one of the fuel types.
title 'The First Five of 171 Observations';
proc print data=sashelp.Gas(obs=5) label;
run;
|
The following statements graph the relationship between the NOx emissions and the equivalence ratio for each fuel type at CpRatio=7.5.
proc sgplot data=sashelp.gas;
where CpRatio=7.5;
scatter y=NOx x=EqRatio / group=fuel markerattrs=(symbol=circlefilled);
title "NOx emissions by Equivalence Ratio";
title2 "CpRatio = 7.5";
run;
The plot shows a nonlinear relationship.
 |
Spline effect specification and the interpretation of output
One possible model for NOx emissions includes a spline transformation for the equivalence ratio. The spline effect is included in the following model by defining the spline, sp_EqRatio, in the EFFECT statement and by specifying sp_EqRatio in the MODEL statement. The WHERE statement excludes two observations with missing values of NOx.
proc glimmix data=sashelp.gas outdesign(x)=Xmatrix;
where Nox ne .;
class Fuel;
effect sp_EqRatio = spline(EqRatio / basis=bspline details);
model NOx = sp_EqRatio CpRatio Fuel / solution;
output out=Out pred=Pred;
run;
The EFFECT statement defines a B-spline expansion for the equivalence ratio. There are three spline bases available in the EFFECT statement: the B-spline (BASIS=BSPLINE, the default), the truncated power function (BASIS=TPF), and the natural cubic spline (NATURALCUBIC). For B- and TPF splines, you can use the DEGREE= option to specify the degree of the spline transformation. The default degree is 3. Natural cubic splines always have DEGREE=3. You can also use the KNOTMETHOD= option to specify how to construct the knots for the spline effects. The default method, EQUAL(3), selects three equally spaced knots that are positioned between the extremes of the data and are referred to as internal knots. For the B-spline basis, there are additional knots placed beyond the data extremes, known as boundary knots. Other knot placement methods include LIST and LISTWITHBOUNDARY which enable you to specify knot values if desired, PERCENTILES to place knots at evenly spaced percentiles of the variable, RANGEFRACTIONS to place knots at specified fractions of the variable's range, and MULTISCALE (for B-splines) to produce sets of B-spline bases with increasing number of knots. See the EFFECT statement documentation for more details about the different knot placement methods.
The EFFECT statement above defines a spline for the equivalence ratio using the default B-spline basis with degree three and three equally spaced internal knots. The values of the B-spline basis functions are contained in the design matrix for X. The OUTDESIGN= option in the PROC GLIMMIX statement saves the design matrix in a SAS data set named Xmatrix. In this example, the B-spline basis functions are in the columns named _X2 through _X8. You can use PROC PRINT to view this data set. The DETAILS option in the EFFECT statement requests tables showing the knot locations and the knots associated with each spline basis function. The "Knots for Spline Effect sp_EqRatio" table shows that the three internal knots are equally spaced between the observed extreme values of 0.535 and 1.267. For the B-spline basis, d boundary knots are positioned to the left of the internal knots, and max(d,1) boundary knots are positioned to the right of the internal knots, where d is the degree of the basis function. In this example, d=3 (the default). By default, the equal spacing of knots is maintained for the boundary knots. However, the actual values of these boundary knots can be arbitrary.
|
|||||||||||||||||||||||||||||||||
The number of basis function is n+d+1, where n is the number of (internal) knots. In this example with d=n=3, the number of functions is 7. In the "Basis Details for Spline Effect sp_EqRatio" table, the Support columns display the range of EqRatio over which each basis function is nonzero. The Support Knots column lists the Knot Numbers (from the previous table) used for the corresponding basis function. For more information about the B-spline basis functions, see the Hastie, Tibshirani, and Friedman (2001) reference cited in the References section of the Shared Concepts and Topics chapter of the SAS/STAT® User's Guide.
|
||||||||||||||||||||||||||||||||||||
In the "Parameter Estimates" table, the values for the sp_EqRatio effect in the Estimate column are the estimated coefficients of the seven basis functions in the B-spline expansion of the equivalence ratio. The coefficients do not generally have meaningful interpretation. They are weights for the individual spline functions, where each function spans a range of the corresponding variable. The weighted sum of such simple functions can closely approximate an arbitrary smooth function, but the individual components and their coefficients are not very helpful in describing that function.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
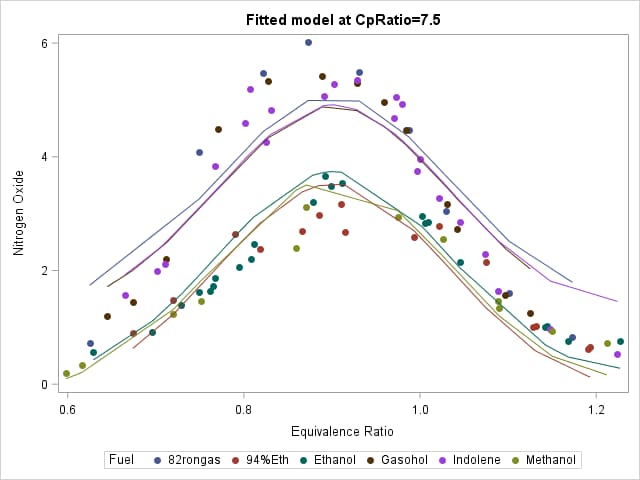
Instead of focusing on the individual coefficients, a graph of the predicted values saved in the OUTPUT OUT= data set enables you to visualize the entire approximated smooth function. The following statements plot the observed and predicted values.
proc sort data=Out;
by Fuel EqRatio;
run;
proc sgplot data=Out;
where cpratio=7.5;
scatter y=NOx x=EqRatio / group=Fuel markerattrs=(symbol=circlefilled);
series y=Pred x=EqRatio / group=Fuel;
title "Fitted model at CpRatio=7.5";
run;
Notice that the fitted model follows the general shape of the data. The above specification of the model uses a single spline, which is shifted up or down for each setting of CpRatio and Fuel. A more complex model that includes interactions of sp_EqRatio with CpRatio and/or Fuel would allow for differently shaped splines at each level of those predictors.
 |
Computing predicted values for (score) new observations
There are four approaches for obtaining predicted values for new observations using a model containing spline effects. See this note for a general discussion of methods for scoring new observations.
- Use the STORE statement to save the fitted model. The PLM procedure can then use the saved model to score the observations without refitting the model each time you want to score a new data set. This approach works for models in PROC GLIMMIX without G-side random effects.
The following statements refit the above model and add a STORE statement to save the fitted model.
proc glimmix data=sashelp.gas; class Fuel; effect sp_EqRatio = spline(EqRatio); model NOx = sp_EqRatio CpRatio Fuel; store out=gmxstore; run;These statements create a data set of new observations to be scored.data temp; input Fuel $ CpRatio EqRatio; datalines; 94%Eth 10 1 Ethanol 13 1.2 ;PROC PLM reads the saved model and the data to score. Predicted values are computed and saved in the variable Pred in data set Scored.proc plm source=gmxstore; score data=Temp out=Scored predicted=Pred; run; - This alternative approach works for all types of models (with or without the G-side random effects in PROC GLIMMIX, for example).
Set the dependent variable to be missing in the data set of observations to be scored.
data Temp; input Fuel $ CpRatio EqRatio; NOx=.; datalines; 94%Eth 10 1 Ethanol 13 1.2 ;Combine (concatenate) the original data and the scoring data set.data Combined; set sashelp.gas Temp; run;Refit your model using this combined data set and save the predicted values. The predicted values for all of the observations in the combined data set, including those from the scoring data set Temp, will be included in the OUT= data set.proc glimmix data=Combined; class Fuel; effect sp_EqRatio = spline(EqRatio); model NOx = sp_EqRatio CpRatio Fuel; output out=out pred=pred; run; - Use SAS programming to reproduce the basis functions and use the estimated model parameters to compute predicted values as discussed and illustrated in SAS Note 57682.
- Individual predicted values can be computed using ESTIMATE statements as illustrated below.
Using the LSMEANS and ESTIMATE statements with spline models
Many procedures that support the EFFECT statement also provide LSMEANS and ESTIMATE statements enabling you to compute least squares means or other linear combinations of model parameters. For models containing fixed spline effects, least squares means are computed at the average spline coefficients across the usable data, possibly further averaged over levels of CLASS variables that interact with the spline effects in the model. You can use the AT option in the LSMEANS (or LSMESTIMATE) statement to construct the splines for particular values of the covariates involved. Consider the following LSMEANS statements:
proc glimmix data=sashelp.gas;
where Nox ne .;
class Fuel;
effect sp_EqRatio = spline(EqRatio);
model NOx = sp_EqRatio CpRatio Fuel;
lsmeans Fuel;
lsmeans Fuel / at means;
lsmeans Fuel / at EqRatio=1;
run;
The "Parameter Estimates" table above shows that the sp_EqRatio spline effect adds seven parameters to the model. Therefore, columns for the seven basis functions (s1, s2,...,s7) are added to the design matrix for the spline effect. In the first LSMEANS statement, the seven sp_EqRatio effect coefficients used in each linear combination are the averages of those columns.
|
||||||||||||||||||||||||||||||||||||||||||||||||
In the second LSMEANS statement, the coefficients for sp_EqRatio are obtained at the average value (0.93) of EqRatio, (s1(0.93), s2(0.93),...,s7(0.93)). The coefficient for CpRatio is the average (10.13) of CpRatio for observations with nonmissing values for NOx.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The final LSMEANS statement uses coefficients for sp_EqRatio at EqRatio=1, (s1(1), s2(1),...,s7(1)), and coefficient for CpRatio at its average (10.13), where NOx is not missing.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
To see the coefficients of the linear combinations defining the least squares means, add the E option in the LSMEANS statement. The AT option can be useful for resolving problems with estimability in least squares means calculations with spline effects.
Since LSMEANS are just linear combinations of model parameters, you can use ESTIMATE statements to reproduce the LSMEANS results. The first LSMEANS statement uses the means of the spline columns and the mean of CpRatio as coefficients. The last two LSMEANS statements use, as coefficients, the means of EqRatio and CpRatio. These statements produce the means of the spline columns, EqRatio, and CpRatio using the saved design matrix.
proc means data=Xmatrix;
where NOx ne .;
run;
|
The following ESTIMATE statements define the same linear combinations of model parameters as the LSMEANS statements above for Fuel=Ethanol. Note that the first ESTIMATE statement uses positional syntax to specify the desired coefficients. Nonpositional syntax is typically used for constructed effects, such as splines, but specifying a contrast equivalent to the one in the first LSMEANS statement using nonpositional syntax would be difficult or impossible. Nonpositional syntax is needed to reproduce the other two LSMEANS statements.
estimate 'Ethanol' Intercept 1
sp_EqRatio 0.0042145 0.0754935 0.2233340 0.2917772 0.2812853 0.1167848 0.0071107
CpRatio 10.1272189 Fuel 0 0 1 0 0 0;
estimate 'Ethanol at means of EqRatio, CpRatio'
Intercept 1 sp_EqRatio [1,0.9283077] CpRatio 10.1272189 Fuel 0 0 1 0 0 0;
estimate 'Ethanol at EqRatio=1, mean CpRatio'
Intercept 1 sp_EqRatio [1,1] CpRatio 10.1272189 Fuel 0 0 1 0 0 0;
Notice that the Ethanol results from the ESTIMATE statements match those from the LSMEANS statements above.
|
||||||||||||||||||||||||||||||
As discussed and illustrated in the Extrapolation section of SAS Note 57682, it is not recommended to compute predicted values outside the range of the data. The following statements also illustrate this problem by predicting values beyond the observed range of EqRatio.
estimate "Ethanol at EqRatio=0.1"
Intercept 1 Fuel 0 0 1 0 0 0 CpRatio 10.1272189 sp_EqRatio [1,0.1];
estimate "Ethanol at EqRatio=0.4"
Intercept 1 Fuel 0 0 1 0 0 0 CpRatio 10.1272189 sp_EqRatio [1,0.4];
estimate "Ethanol at EqRatio=1.5"
Intercept 1 Fuel 0 0 1 0 0 0 CpRatio 10.1272189 sp_EqRatio [1,1.5];
estimate "Ethanol at EqRatio=5"
Intercept 1 Fuel 0 0 1 0 0 0 CpRatio 10.1272189 sp_EqRatio [1,5];
For the B-spline basis, all EqRatio values to the left of the data range are assigned the value of 1 for the first spline basis function and 0 for all other spline basis functions. All EqRatio values to the right of the data range are assigned the value of 1 for the last spline basis function and 0 for all other spline basis functions. As a result, the predicted values are the same for EqRatio=0.1 and EqRatio=0.4 since they are less than the smallest EqRatio value in the data. Similarly, the predicted values are the same for EqRatio=1.5 and EqRatio=5 since they are greater than the largest EqRatio value in the data.
|
||||||||||||||||||||||||||||||||||||
Truncated power function and natural cubic splines have different rules for observations outside the range of the data, but because of the flexibility of splines, all of them can produce unreasonable estimates outside the range of the data. As a result, such extrapolation is not recommended.
To assess the effect of changing the splined variable by one or more units, see SAS Notes 67024 and 70221.
Operating System and Release Information
| Product Family | Product | System | SAS Release | |
| Reported | Fixed* | |||
| SAS System | SAS/STAT | Solaris | ||
| OpenVMS on HP Integrity | ||||
| OpenVMS Alpha | ||||
| Linux for x64 | ||||
| Linux | ||||
| IRIX | ||||
| HP-UX | ||||
| AIX | ||||
| ABI+ for Intel Architecture | ||||
| 64-bit Enabled Solaris | ||||
| 64-bit Enabled HP-UX | ||||
| 64-bit Enabled AIX | ||||
| Windows Vista for x64 | ||||
| Windows Vista | ||||
| Windows Millennium Edition (Me) | ||||
| Windows 7 Ultimate x64 | ||||
| Windows 7 Ultimate 32 bit | ||||
| Windows 7 Professional x64 | ||||
| Windows 7 Professional 32 bit | ||||
| Windows 7 Home Premium x64 | ||||
| Windows 7 Home Premium 32 bit | ||||
| Windows 7 Enterprise x64 | ||||
| Microsoft Windows Server 2008 R2 | ||||
| Microsoft Windows Server 2008 | ||||
| Microsoft Windows Server 2003 for x64 | ||||
| Microsoft Windows Server 2003 Standard Edition | ||||
| Microsoft Windows Server 2003 Enterprise Edition | ||||
| Microsoft Windows 10 | ||||
| Microsoft Windows 8.1 Enterprise x64 | ||||
| Microsoft Windows 8.1 Enterprise 32-bit | ||||
| Microsoft Windows 8 Pro x64 | ||||
| Microsoft Windows 8 Pro 32-bit | ||||
| Microsoft Windows 8 Enterprise x64 | ||||
| OS/2 | ||||
| Microsoft® Windows® for x64 | ||||
| Microsoft Windows XP 64-bit Edition | ||||
| Microsoft Windows Server 2003 Datacenter 64-bit Edition | ||||
| Microsoft® Windows® for 64-Bit Itanium-based Systems | ||||
| OpenVMS VAX | ||||
| z/OS 64-bit | ||||
| Linux on Itanium | ||||
| HP-UX IPF | ||||
| Windows 7 Enterprise 32 bit | ||||
| Microsoft Windows XP Professional | ||||
| Microsoft Windows Server 2012 Std | ||||
| Microsoft Windows Server 2012 R2 Std | ||||
| Microsoft Windows Server 2012 R2 Datacenter | ||||
| Microsoft Windows Server 2012 Datacenter | ||||
| Microsoft Windows Server 2008 for x64 | ||||
| Microsoft Windows Server 2003 Datacenter Edition | ||||
| Microsoft Windows NT Workstation | ||||
| Microsoft Windows 2000 Professional | ||||
| Microsoft Windows 2000 Server | ||||
| Microsoft Windows 2000 Datacenter Server | ||||
| Microsoft Windows 2000 Advanced Server | ||||
| Microsoft Windows 95/98 | ||||
| Microsoft Windows 8.1 Pro x64 | ||||
| Microsoft Windows 8.1 Pro 32-bit | ||||
| Microsoft Windows 8 Enterprise 32-bit | ||||
| Microsoft Windows Server 2003 Enterprise 64-bit Edition | ||||
| z/OS | ||||
| Solaris for x64 | ||||
| Tru64 UNIX | ||||
| Type: | Usage Note |
| Priority: | |
| Topic: | Analytics ==> Nonparametric Analysis Analytics ==> Transformations SAS Reference ==> Procedures ==> GLIMMIX SAS Reference ==> Procedures ==> GLMSELECT SAS Reference ==> Procedures ==> HPMIXED SAS Reference ==> Procedures ==> LOGISTIC SAS Reference ==> Procedures ==> ORTHOREG SAS Reference ==> Procedures ==> PHREG SAS Reference ==> Procedures ==> PLS SAS Reference ==> Procedures ==> QUANTREG SAS Reference ==> Procedures ==> QUANTSELECT SAS Reference ==> Procedures ==> ROBUSTREG SAS Reference ==> Procedures ==> SURVEYLOGISTIC SAS Reference ==> Procedures ==> SURVEYREG |
| Date Modified: | 2023-07-07 17:20:34 |
| Date Created: | 2016-04-01 11:06:17 |