Usage Note 50700: Design and analysis of equivalence tests
 |  |  |
In a test of equivalence, the means for a new and a reference treatment are compared to try to show that the treatments are the same. Equivalence tests are often used in bioequivalence studies in which two drugs are compared with the intent to show that the new drug is the same as a standard drug.
Under the null hypothesis of an equivalence test, the treatment means differ by more than some practically unimportant amount called the margin. Under the alternative hypothesis, the means differ by less than this amount and are therefore considered equivalent for practical purposes. Since the power of a test is the probability of rejecting the null hypothesis when the alternative is true, the power in an equivalence test is the probability of rejecting nonequivalence when the treatments are in fact equivalent. That is, it is the probability of observing a difference (or ratio) of treatment means within the margin when the true values are within the margin. Equivalence tests are further introduced along with the related inferiority and superiority tests in this note.
Design and analysis tools for equivalence tests
Power analysis and sample size determination for equivalence tests can be done in PROC POWER for the following situations. Analysis of data from an equivalence study can be conducted using PROC FREQ or PROC TTEST.
| Type of Test | PROC POWER Statement | Analysis Procedure | Required Statement |
|---|---|---|---|
| One-sample test of mean | ONESAMPLEMEANS | TTEST | |
| Two-sample comparison of means | TWOSAMPLEMEANS | TTEST | CLASS |
| Paired-sample comparison of means | PAIREDMEANS | TTEST | PAIRED |
| One-sample test of proportion | ONESAMPLEFREQ | FREQ | TABLE BINOMIAL(EQUIV MARGIN=) |
| Two-sample comparison of proportions | Not available | FREQ | TABLE RISKDIFF(EQUIV MARGIN=) |
| Paired-sample comparison of proportions | Not available |
The following examples illustrate designing equivalence studies and conducting equivalence tests. Additional examples of power and sample size computations for equivalence tests using the ONESAMPLEMEANS, TWOSAMPLEMEANS, PAIREDMEANS, and ONESAMPLEFREQ statements are available in the descriptions of these statements in the PROC POWER documentation.
One-Sample Equivalence Test: The ONESAMPLEMEANS Statement
Suppose a cereal company wants to test whether a new packaging machine produces boxes with weight equivalent to a target value of 14 ounces per box. Weight is assumed to be normally distributed and the researchers decide that a meaningful difference from the target must exceed 0.2 oz. in either direction. The standard deviation of the weight is about 0.5 oz. What is the sample size needed in an 0.05 level equivalence test with 90% power to conclude the weight is within the margin?
The hypotheses for a one-sample equivalence test are:
H0: μ < θL or μ > θU
H1: θL ≤ μ ≤ θU
where μ is the mean weight from the new machine. With target value μ0 and margin m, θL=μ0-m and θU=μ0+m are the lower and upper bounds specified in the LOWER= and UPPER= options in the ONESAMPLEMEANS statement in PROC POWER. Following the two one-sided tests (TOST) procedure of Schuirmann (1987), the equivalence test is conducted by performing two separate tests, L and U:
H0L: μ < θL
H1L: μ ≥ θL
and
H0U: μ > θU
H1U: μ ≤ θU
The overall p-value of the equivalence test is the larger of the two p-values of tests L and U. Rejection of H0 in favor of H1 at significance level α occurs if and only if the 100(1-2α)% confidence interval for μ is contained completely within (θL, θU).
For this example with μ0=14 and m=0.2, the hypotheses are
H0: μ < 13.8 or μ > 14.2
H1: 13.8 ≤ μ ≤ 14.2
The following statements compute the sample size for this equivalence test.
proc power;
onesamplemeans test=equiv
lower = 13.8
upper = 14.2
mean = 14
stddev = 0.5
ntotal = .
power = 0.9
alpha = 0.05;
run;
The results show that a sample size of 70 is required to have 90% power for this equivalence test.
|
The POWER Procedure
Equivalence Test for Normal Mean
| ||||||||||||||||||||||||
Suppose weight measurements are obtained from 70 randomly selected cereal boxes. These statements create a data set of the observed box weights.
data BoxWts;
input weight @@;
datalines;
14.15 13.68 13.58 14.26 14.29
14.32 13.56 14.03 12.68 13.58
14.13 14.37 14.11 13.94 14.11
14.27 13.92 14.50 14.05 13.77
14.60 14.18 14.07 14.15 13.82
13.76 14.28 13.67 14.58 14.83
13.71 13.31 13.46 14.12 14.14
13.05 14.08 13.98 14.04 14.33
13.42 14.00 13.70 14.09 14.12
13.48 13.70 14.11 14.14 13.17
13.82 13.55 13.54 13.11 13.92
13.56 14.08 13.17 14.52 14.23
14.22 13.82 13.64 14.32 14.31
13.55 13.58 13.25 14.34 14.02
;
The following statements use PROC TTEST to perform the equivalence test. The TOST option requests the two one-sided equivalence test. The equivalence bounds are specified in parentheses.
proc ttest data=BoxWts tost(13.8, 14.2);
var weight;
run;
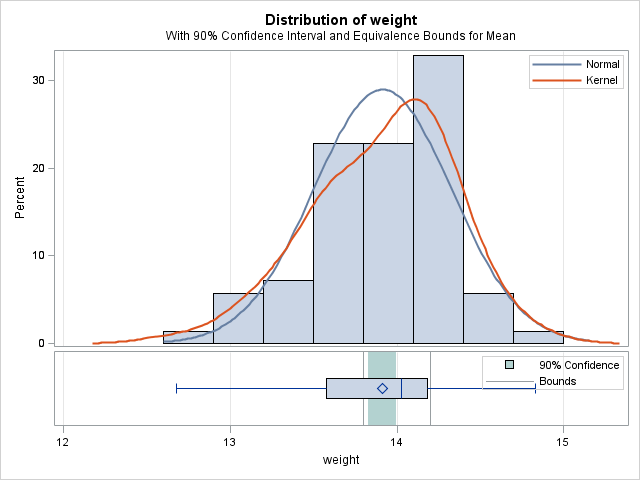
The average weight of the sampled boxes is 13.91 oz. The equivalence test finds significant evidence that the true mean weight is equivalent to the target (p=0.0124). This is visually apparent since the 90% confidence interval (13.83, 14.00) on the mean weight is completely contained within the equivalence bounds.
|
TOST Level 0.05 Equivalence Analysis
| ||||||||||||||||||||||||||||||||||||
Paired-Sample Equivalence Test: The PAIREDMEANS Statement
In a study hoping to show that exposure to a substance has no effect on subjects, subject responses are recorded before and after exposure. The response values are assumed to be have a lognormal distribution. A 0.05 level equivalence test with 90% power is proposed to test that the ratio of the mean responses is within equivalence bounds [0.8, 1.25]. The correlation between the measurements within subjects is assumed to be 0.6 based on previous similar studies. It is desired to explore the sample sizes needed for a range of CV (Coefficient of Variation = standard deviation / mean) values common to both groups. Based on prior knowledge of this substance, a range of CV values between 0.2 and 0.3 is assumed, and a range of possible mean ratios from 0.85 to 1.15 is of interest.
The mean ratio refers to the ratio of the geometric means from the two groups. For definitions of arithmetic and geometric means, see "Computational Methods: Arithmetic and Geometric Means" in the Details section of the TTEST procedure documentation. Along with the correlation, the CV specifies the variability in lognormal data. The CV is assumed to be common to both groups, and the standard deviation and mean in the CV formula are the arithmetic mean and standard deviation of the original data. CV relates to the variance of the log-transformed data, v, as CV = sqrt(exp(v)-1). See "Computational Methods: Coefficient of Variation" in the Details section of the TTEST documentation for more information.
The following statements compute and plot the sample sizes for several CV-mean ratio scenarios using the PAIREDMEANS statement. The TEST=EQUIV_RATIO option requests power analysis for an equivalence test based on the ratio of means. Note that for an equivalence test the specified ALPHA= value provides the sample size for a (1-2α)100% confidence interval on the mean ratio. The PLOT statement plots the number of pairs needed for each of the scenarios.
proc power;
pairedmeans test=equiv_ratio
lower = 0.8
upper = 1.25
meanratio = 0.85 to 1.15 by 0.05
cv = 0.2 0.23 0.25 0.3
corr = 0.6
npairs = .
alpha = 0.05
power = 0.90;
plot x=effect step=0.05
vary(color by cv) yopts=(ref=10 to 170 by 10);
run;
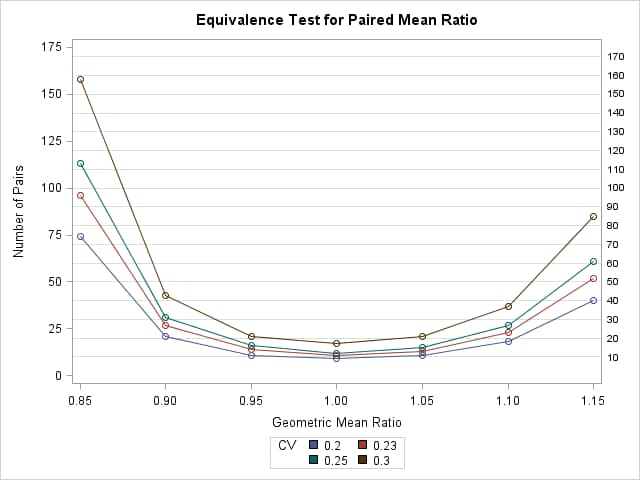
Results of the power analysis shows that the larger the CV or the farther the mean ratio is from 1, the larger sample size required for the equivalence test.
|
The POWER Procedure
Equivalence Test for Paired Mean Ratio
|
Suppose researchers decide that the most likely CV and mean ratio values will call for a sample size of 20. They proceed to conduct the study with 20 patients and the resulting measurements from each subject before and after exposure are recorded in the following data set.
data Responses;
input Subject Before After @@;
datalines;
1 21.84 25.05 11 18.41 23.87
2 22.42 24.22 12 26.21 26.02
3 20.38 23.85 13 19.11 21.88
4 20.30 16.61 14 16.51 22.26
5 19.08 22.04 15 26.15 20.21
6 22.35 29.32 16 16.78 20.13
7 19.63 17.55 17 18.67 19.44
8 21.18 16.94 18 22.14 22.61
9 24.75 22.70 19 22.37 22.45
10 14.45 11.27 20 20.33 22.84
;
The equivalence test for paired samples is performed using the PAIRED statement in PROC TTEST.
proc ttest data=Responses dist=lognormal tost(0.8, 1.25);
paired before*after;
run;
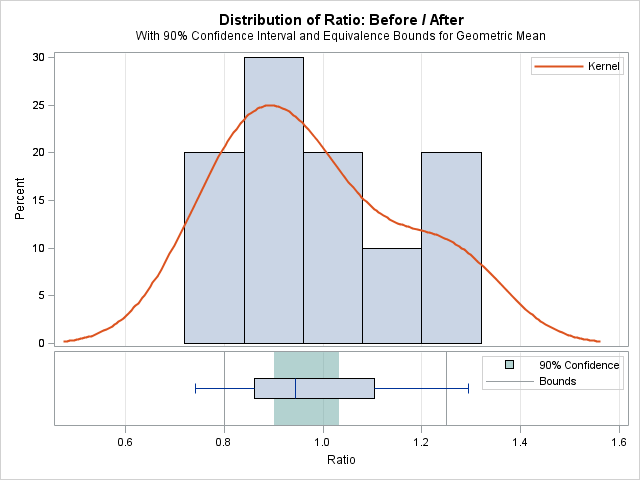
The nonequivalence null hypothesis is rejected (p<0.0001) indicating significant evidence for equivalent means before and after exposure and implying no effect due to exposure to the substance.
|
TOST Level 0.05 Equivalence Analysis
| ||||||||||||||||||||||||||||||||||||
Operating System and Release Information
| Product Family | Product | System | SAS Release | |
| Reported | Fixed* | |||
| SAS System | SAS/STAT | Microsoft® Windows® for 64-Bit Itanium-based Systems | ||
| Z64 | ||||
| z/OS | ||||
| OpenVMS VAX | ||||
| Microsoft Windows Server 2003 Datacenter 64-bit Edition | ||||
| Microsoft Windows Server 2003 Enterprise 64-bit Edition | ||||
| Microsoft Windows XP 64-bit Edition | ||||
| Microsoft® Windows® for x64 | ||||
| OS/2 | ||||
| Microsoft Windows 8 Enterprise 32-bit | ||||
| Microsoft Windows 8 Enterprise x64 | ||||
| Microsoft Windows 8 Pro 32-bit | ||||
| Microsoft Windows 8 Pro x64 | ||||
| Microsoft Windows 95/98 | ||||
| Microsoft Windows 2000 Advanced Server | ||||
| Microsoft Windows 2000 Datacenter Server | ||||
| Microsoft Windows 2000 Server | ||||
| Microsoft Windows 2000 Professional | ||||
| Microsoft Windows NT Workstation | ||||
| Microsoft Windows Server 2003 Datacenter Edition | ||||
| Microsoft Windows Server 2003 Enterprise Edition | ||||
| Microsoft Windows Server 2003 Standard Edition | ||||
| Microsoft Windows Server 2003 for x64 | ||||
| Microsoft Windows Server 2008 | ||||
| Microsoft Windows Server 2008 R2 | ||||
| Microsoft Windows Server 2008 for x64 | ||||
| Microsoft Windows Server 2012 Datacenter | ||||
| Microsoft Windows Server 2012 Std | ||||
| Microsoft Windows XP Professional | ||||
| Windows 7 Enterprise 32 bit | ||||
| Windows 7 Enterprise x64 | ||||
| Windows 7 Home Premium 32 bit | ||||
| Windows 7 Home Premium x64 | ||||
| Windows 7 Professional 32 bit | ||||
| Windows 7 Professional x64 | ||||
| Windows 7 Ultimate 32 bit | ||||
| Windows 7 Ultimate x64 | ||||
| Windows Millennium Edition (Me) | ||||
| Windows Vista | ||||
| Windows Vista for x64 | ||||
| 64-bit Enabled AIX | ||||
| 64-bit Enabled HP-UX | ||||
| 64-bit Enabled Solaris | ||||
| ABI+ for Intel Architecture | ||||
| AIX | ||||
| HP-UX | ||||
| HP-UX IPF | ||||
| IRIX | ||||
| Linux | ||||
| Linux for x64 | ||||
| Linux on Itanium | ||||
| OpenVMS Alpha | ||||
| OpenVMS on HP Integrity | ||||
| Solaris | ||||
| Solaris for x64 | ||||
| Tru64 UNIX | ||||