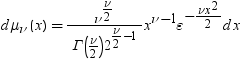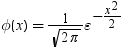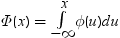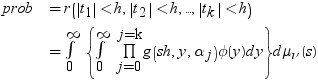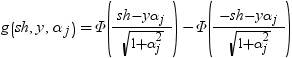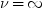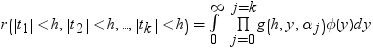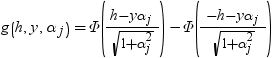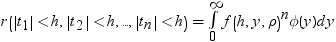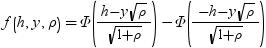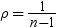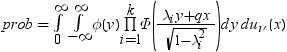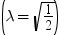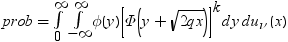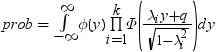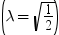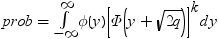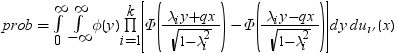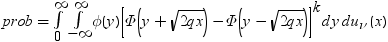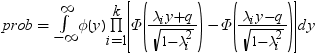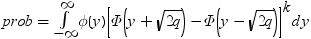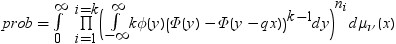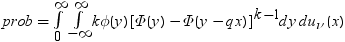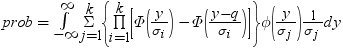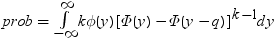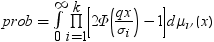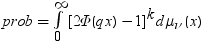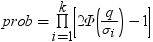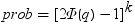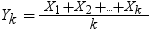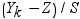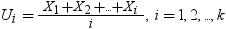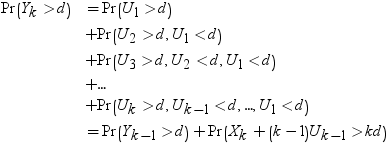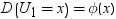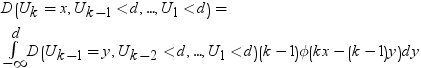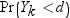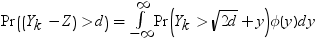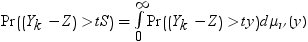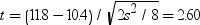PROBMC関数
平均値の多重比較を行うために各種の分布から確率または分位点を返します。
| カテゴリ: | 確率 |
構文
詳細
平均分析の計算
平均分析(ANOM)は、i番目のサンプルサイズがniとなるk(ガウス)サンプルのデータで使用されます。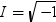
のようになります。分布関数[1, 2, 3, 4, 5]はk次元の多変量
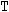ベクトルの最大絶対値のCDFです。このとき、自由度は 
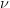、関連相関行列は 
です。この式は次のように表すことができます。
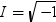のようになります。分布関数[1, 2, 3, 4, 5]はk次元の多変量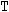ベクトルの最大絶対値のCDFです。このとき、自由度は 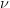、関連相関行列は です。この式は次のように表すことができます。
前述の式には次の関係が適用されます。
, 
および
はそれぞれ正規分布のガンマ関数、密度およびCDFです。
のとき、分布は次に減少します。
前述の式には次の関係が適用されます。
均衡しているケースでは、分布は次に減少します。
前述の式には次の関係が適用されます。
および 
この分布の構文は次のとおりです。
x=probmc('anom', q, p, nu, n, <alpha1 , ..., alphan>);
引数
x
返される結果の数値です。
q
分位点を示す数値です。
p
確率を示す数値です。pとqは、いずれかが欠損値である必要があります。
nu
自由度を示す数値です。
n
サンプル数を示す数値です。
alphai, i=1,...,k
この分布の最初の式のα値を示す数値です(省略可能)。平均分析の計算を参照してください。.
分割された範囲の計算
RANGEは、nのグループ平均のスチューデント化範囲の分布で使用されます。PARTRANGEは、分割されたスチューデント化範囲の分布で使用されます。nグループを、大きさがn1+ ...+ nk= nのk個のサブセットに分割します。このとき、分割された範囲はそれぞれのサブセットのスチューデント化範囲の最大です。スチューデント化係数はすべてのケースで同一です。
この分布の構文は次のとおりです。
x=probmc('partrange', q, p, nu, k, n1, ..., nk);
引数
x
返される結果の数値です(確率または分位点)。
q
分位点を示す数値です。
p
確率を示す数値です。pとqは、いずれかが欠損値である必要があります。
nu
自由度を示す数値です。
k
グループ数を示す数値です。
ni i=1,...,k
この分布の式のn値を示す数値です(省略可能)。分割された範囲の計算を参照してください。
Williams検定
PROBMCは、Williams (1971、1972)によって定義されている分布の確率または分位点を計算します。(リファレンスを参照。) 処方治療の平均をコントロール平均と比較し、治療で有効な最小の処方量を判断するため使用します。
注: Williams検定はサンプルサイズが揃っているときにのみ計算されます。
X1, X2, ..., Xkは同一の独立しているN(0,1)の確率変数であるものとします。Ykは次の式で表されるそれらの平均であるものとします。
次の分布を計算する必要があります。
引数
Yk
前述の定義のとおりです。
Z
N(0,1)の独立した確率変数です。
S
½νS2がχ2変数です(自由度ν)。
Williams (1971) (リファレンス を参照)の説明によれば、全体の計算は非常に冗長であり、3段階で行われます。
ν = ∞のときは、第3段階は必要ありません。演算が複雑なため、この冗長なアルゴリズムは有限および無限の自由度νの両方でk ≤ 15のとき、高速なアルゴリズムに置き換えられます。k≥ 16のときは、冗長計算が実行されます。この計算は、アルゴリズムが複雑なため、きわめて高コストで非常に時間がかかります。
例
例1: PROBMCを使用した確率の計算
次の例では、確率の計算方法を示します。
data probs;
array par{5};
par{1}=.5;
par{2}=.51;
par{3}=.55;
par{4}=.45;
par{5}=.2;
df=40;
q=1;
do test="dunnett1","dunnett2", "maxmod";
prob=probmc(test, q, ., df, 5, of par1–par5);
put test $10. df q e18.13 prob e18.13;
end;
run; SASは次の結果をログに書き込みます。
DUNNETT1 40 1.00000000000E+00 4.82992196083E-01 DUNNETT2 40 1.00000000000E+00 1.64023105316E-01 MAXMOD 40 1.00000000000E+00 8.02784203408E-01
例2: 平均分析の計算
data _null_;
q1=probmc('anom', ., 0.9, ., 20); put q1=;
q2=probmc('anom', ., 0.9, 20, 5, 0.1, 0.1, 0.1, 0.1, 0.1); put q2=;
q3=probmc('anom', ., 0.9, 20, 5, 0.5, 0.5, 0.5, 0.5, 0.5); put q3=;
q4=probmc('anom', ., 0.9, 20, 5, 0.1, 0.2, 0.3, 0.4, 0.5); put q4=;
run;SASは次の結果をログに書き込みます。
q1=2.7895061016 q2=2.4549961967 q3=2.4549961967 q4=2.4532319994
例3: 平均の比較
この例では、グループ平均を比較して有意な差異がどこにあるかを調べる方法を示します。この例のデータはDuncan (1955)の論文から引用しています。また、Hochberg
and Tamhane (1987)にも記載されています。(この関数の末尾のリファレンスセクションを参照してください。)
次の値はグループ平均です。
このデータでは、平均平方誤差はν = 30のときs2 = 79.64 (s = 8.924)です。
-
49.6
-
71.2
-
67.6
-
61.5
-
71.3
-
58.1
-
61.0
data duncan;
array tr{7}$;
array mu{7};
n=7;
do i=1 to n;
input tr{i} $1. mu{i};
end;
input df s alpha;
prob=1-alpha;
/* compute the interval */
x=probmc("RANGE", ., prob, df, 7);
w=x * s / sqrt(6);
/* compare the means */
do i=1 to n;
do j=i + 1 to n;
dmean = abs(mu{i} - mu{j});
if dmean >= w then do;
put tr{i} tr{j} dmean;
end;
end;
end;
datalines;
A 49.6
B 71.2
C 67.6
D 61.5
E 71.3
F 58.1
G 61.0
30 8.924 .05
;
run;SASは次の結果をログに書き込みます。
A B 21.6 A C 18 A E 21.7
例4
data _null_;
q1=probmc('partrange', ., 0.9, ., 4, 3, 4, 5, 6); put q1=;
q2=probmc('partrange', ., 0.9, 12, 4, 3, 4, 5, 6); put q2=;
run;SASは次の結果をログに書き込みます。
q1=4.1022397989 q2=4.7888626338
例5: 信頼区間の計算
この例では、Dunnett検定の片側検定と両側検定で95%信頼区間を計算する方法を示します。この例およびデータはDuncan (1955)の論文から引用しています。また、Hochberg
and Tamhane (1987)にも記載されています。(この関数の末尾のリファレンスセクションを参照してください。)データは、3つの動物グループの血球数測定値です。次の表に示すとおり、第3グループをコントロールグループとして、最初の2つのグループには異なる薬物を投与します。3つのグループの動物の数は不揃いです。
|
投与グループ:
|
薬物A
|
薬物B
|
コントロール
|
|---|---|---|---|
|
|
9.76
|
12.80
|
7.40
|
|
|
8.80
|
9.68
|
8.50
|
|
|
7.68
|
12.16
|
7.20
|
|
|
9.36
|
9.20
|
8.24
|
|
|
|
10.55
|
9.84
|
|
|
|
|
8.32
|
|
グループ平均
|
8.90
|
10.88
|
8.25
|
|
n
|
4
|
5
|
6
|
平均平方誤差はν = 12のときs2 = 1.3805 (s = 1.175)です。
data a;
array drug{3}$;
array count{3};
array mu{3};
array lambda{2};
array delta{2};
array left{2};
array right{2};
/* input the table */
do i=1 to 3;
input drug{i} count{i} mu{i};
end;
/* input the alpha level, */
/* the degrees of freedom, */
/* and the mean square error */
input alpha df s;
/* from the sample size, */
/* compute the lambdas */
do i=1 to 2;
lambda{i}=sqrt(count{i}/
(count{i} + count{3}));
end;
/* run the one-sided Dunnett's test */
test="dunnett1";
x=probmc(test, ., 1 - alpha, df,
2, of lambda1-lambda2);
do i=1 to 2;
delta{i}=x * s *
sqrt(1/count{i} + 1/count{3});
left{i}=mu{i} - mu{3} - delta{i};
end;
put test $10. x left{1} left{2};
/* run the two-sided Dunnett's test */
test="dunnett2";
x=probmc(test, ., 1 - alpha, df,
2, of lambda1-lambda2);
do i=1 to 2;
delta{i}=x * s *
sqrt(1/count{i} + 1/count{3});
left{i}=mu{i} - mu{3} - delta{i};
right{i}=mu{i} - mu{3} + delta{i};
end;
put test $10. left{1} right{1};
put test $10. left{2} right{2};
datalines;
A 4 8.90
B 5 10.88
C 6 8.25
0.05 12 1.175
;
run;SASは次の結果をログに書き込みます。
DUNNETT1 2.1210448226 -0.958726041 1.1208812046 DUNNETT2 -1.256408109 2.5564081095 DUNNETT2 0.8416306717 4.4183693283
例6: Williams検定の計算
次の例では、8つのブロックからなる乱塊法を使用し、7つの水準である物質を検定しました。観測された処理の平均は次のとおりです。
自由度は(7 – 1)(8 – 1) = 42で、平均平方はs2 = 1.16です。
平均化プロセスを経て最大尤度推定Miを求めます。
-
X0 > X1であるから、X0,1 = (X0 + X1)/2 = 10.15である。
-
X0,1 > X2であるから、X0,1,2 = (X0 + X1 + X2)/3=(2X0,1 + X2)/3=10.1である。
-
X0,1,2 < X3 < X4 < X5
-
X5 > X6であるから、X5,6 = (X5 + X6)/2 = 11.8である。
これで順序制約が満たされました。
対立仮説では、最大尤度推定は次のとおりです。
-
M0=M1=M2 = X0,1,2=10.1
-
M3=X3=10.6
-
M4=X4=11.4
-
M5=M6=X5,6=11.8
次に 
を計算すると、k = 6、ν = 42、t = 2.60に対応する確率は.9924467341となります。すなわち、物質に対する強い反応があることが示されています。また、次の表に示すように、上の5%および裾の1%の分位点も計算できます。
を計算すると、k = 6、ν = 42、t = 2.60に対応する確率は.9924467341となります。すなわち、物質に対する強い反応があることが示されています。また、次の表に示すように、上の5%および裾の1%の分位点も計算できます。
参考文献
“On the Computation of the Distribution for the Analysis of Means.” 2004. Communications in Statistics:Simulation and Computation 33: 861–887.
“Numerical Evaluation of an Equicorrelated Multivariate Non-central t Distribution.”
1981. Communications in Statistics:Part B - Simulation and Computation 10: 41–50.
“Exact Critical Points for the Analysis of Means.” 1982. Communications in Statistics:Part A - Theory and Methods 11: 699–709.
“An Approximation for the Complex Normal Probability Integral.” 1982a. BIT 22(1): 94-255.
“Application of the Analysis of Means.” 1988. Proceedings of the SAS Users Group International Conference 13: 225–230.
“Numerical Evaluation of Multivariate Normal Integrals with Correlations.” 1991. The Frontiers of Statistical Scientific Theory and Industrial Applications 2: 97–114.
“Additional Uses for the Analysis of Means and Extended Tables of Critical Values.”
1993. Technometrics 35: 61-255.