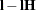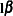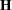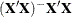The SURVEYREG Procedure

CONTRAST Statement

CONTRAST ’label’ effect values </ options>;

CONTRAST ’label’ effect values <…effect values> </ options>;

The CONTRAST statement provides custom hypothesis tests for linear combinations of the regression parameters 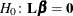$H_{0}\colon \mb{L} \bbeta = \mb{0}$ , where $\mb{L}$ is the vector or matrix you specify and $\bbeta$ is the vector of regression parameters. Thus, to use this feature, you must be familiar with the details of the model parameterization used by PROC SURVEYREG. For information about the parameterization, see the section GLM Parameterization of Classification Variables and Effects in Chapter 19: Shared Concepts and Topics.

Each term in the MODEL statement, called an effect, is a variable or a combination of variables. You can specify an effect with a variable name or a special notation by using variable names and operators. For more details about how to specify an effect, see the section Specification of Effects in Chapter 46: The GLM Procedure.

For each CONTRAST statement, PROC SURVEYREG computes Wald’s F test. The procedure displays this value with the degrees of freedom, and identifies it with the contrast label. The numerator degrees of freedom for Wald’s F test equal rank( $\mb{L}$ ). The denominator degrees of freedom equal the number of clusters (or the number of observations if there is no CLUSTER statement) minus the number of strata. Alternatively, you can use the DF= option in the MODEL statement to specify the denominator degrees of freedom.

You can specify any number of CONTRAST statements, but they must appear after the MODEL statement.

In the CONTRAST statement,

label: identifies the contrast in the output. A label is required for every contrast specified. Labels must be enclosed in single quotes.
effect: identifies an effect that appears in the MODEL statement. You can use the INTERCEPT keyword as an effect when an intercept is fitted in the model. You do not need to include all effects that are in the MODEL statement.
values: are constants that are elements of $\mb{L}$ associated with the effect.

You can specify the following options in the CONTRAST statement after a slash (/):

E

displays the entire coefficient $\mb{L}$ vector or matrix.

NOFILL

requests no filling in higher-order effects. When you specify only certain portions of $\mb{L}$ , by default PROC SURVEYREG constructs the remaining elements from the context. (For more information, see the section Specification of ESTIMATE Expressions in Chapter 46: The GLM Procedure.)

When you specify the NOFILL option, PROC SURVEYREG does not construct the remaining portions and treats the vector or matrix $\mb{L}$ as it is defined in the CONTRAST statement.

SINGULAR=value

tunes the estimability checking. If $\mb{v}$ is a vector, define ABS( $\mb{v}$ ) to be the largest absolute value of the elements of $\mb{v}$ . For a row vector $\mb{l}$ of the matrix $\mb{L}$ , define

$c=\left\{ {\begin{array}{ll} \mbox{ABS}(\mb{l}) & \mbox{if ABS}(\mb{l}) > 0 \\ 1 & \mbox{otherwise} \end{array} } \right.$

If ABS( $\mb{l} - \mb{lH}$ ) is greater than c*value, then $\mb{l}\bbeta$ is declared nonestimable. Here, $\mb{H}$ is the matrix $(\mb{X}’\mb{X})^{-}\mb{X}’\mb{X}$ . The value must be between 0 and 1; the default is $10^{-7}$ .

As stated previously, the CONTRAST statement enables you to perform hypothesis tests $H_{0}\colon \mb{L} \bbeta = 0$ .

If the $\mb{L}$ matrix contains more than one contrast, then you can separate the rows of the $\mb{L}$ matrix with commas.

For example, for the model

proc surveyreg;
   class A B;
   model Y=A B;
run;

with A at 5 levels and B at 2 levels, the parameter vector is

$(\mu ~ ~ \alpha _1 ~ ~ \alpha _2 ~ ~ \alpha _3 ~ ~ \alpha _4 ~ ~ \alpha _5 ~ ~ \beta _1 ~ ~ \beta _2)$

To test the hypothesis that the pooled A linear and A quadratic effect is zero, you can use the following $\mb{L}$ matrix:

$\mb{L} = \left[ \begin{array}{rrrrrrrr} 0 & -2 & -1 & 0 & 1 & ~ 2 & ~ 0 & ~ 0 \\ 0 & 2 & -1 & -2 & -1 & ~ 2 & ~ 0 & ~ 0 \\ \end{array} \right]$

The corresponding CONTRAST statement is

contrast 'A Linear & Quadratic'
         a -2 -1  0  1  2,
         a  2 -1 -2 -1  2;