The STDRATE Procedure

Mantel-Haenszel Effect Estimation

Subsections:

In direct standardization, the derived standardized rates and risks in a study population are the weighted average of the stratum-specific rates and risks in the population, respectively, where the weights are given by the population-time for standardized rate and the number of observations for standardized risk in a reference population.

Assuming that an effect, such as rate difference, rate ratio, risk difference, and risk ratio between two populations, is homogeneous across strata, the Mantel-Haenszel estimates of this effect can be constructed from directly standardized rates or risks in the two populations, where the weights are constructed from the stratum-specific population-times for rate and number of observations for risk of the two populations.

That is, for population k, k=1 and 2, the standardized rate and risk are

\[ {\hat\lambda }_{k} = \frac{ \sum _{j} w_ j \, {\hat\lambda }_{kj} }{ \sum _{j} w_ j } \; \; \; \; \; \mbox{and} \; \; \; \; \; {\hat\gamma }_{k} = \frac{ \sum _{j} w_ j \, {\hat\gamma }_{kj} }{ \sum _{j} w_ j } \]

where the weights are

\[ w_ j = \frac{{\mathcal T}_{1j} \, {\mathcal T}_{2j}}{{\mathcal T}_{1j} + {\mathcal T}_{2j}} \]

for standardized rate, and

\[ w_ j = \frac{{\mathcal N}_{1j} \, {\mathcal N}_{2j}}{{\mathcal N}_{1j} + {\mathcal N}_{2j}} \]

for standardized risk.

Rate and Risk Difference Statistics

Denote 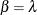$\beta =\lambda $ for rate and 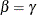$\beta =\gamma $ for risk. The variance is

\[ V( {\hat\beta }_{k} ) = V \left( \frac{ \sum _{j} w_ j \, {\hat\beta }_{kj} }{ \sum _{j} w_ j } \right) = \frac{1}{ (\sum _{j} w_ j)^{2} } \; \, \sum _{j} w_ j^{2} \, V( {\hat\beta }_{kj} ) \]

The Mantel-Haenszel difference statistic is

\[ {\hat\beta }_{1} - {\hat\beta }_{2} \]

with variance

\[ V( {\hat\beta }_{1} - {\hat\beta }_{2} ) = V( {\hat\beta }_{1} ) + V( {\hat\beta }_{2} ) \]

Under the null hypothesis 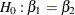$H_0: {\beta }_{1} = {\beta }_{2}$, the difference statistic 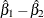${\hat\beta }_{1} - {\hat\beta }_{2}$ has a normal distribution with mean 0.

Rate Ratio Statistic

The Mantel-Haenszel rate ratio statistic is 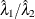${\hat\lambda }_{1} / {\hat\lambda }_{2}$, and the log ratio statistic is

\[ \mbox{log} \left( \frac{{\hat\lambda }_{1}}{{\hat\lambda }_{2}} \right) \]

Under the null hypothesis 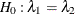$H_0: {\lambda }_{1} = {\lambda }_{2}$ (or equivalently, 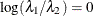$\mbox{log} ({\lambda }_{1} / {\lambda }_{2}) = 0$), the log ratio statistic has a normal distribution with mean 0 and variance

\[ V \left( \mbox{log} \left( \frac{{\hat\lambda }_{1}}{{\hat\lambda }_{2}} \right) \right) = \frac{ \sum _{j} w_ j \, {\hat\lambda }_{pj} }{ (\sum _{j} w_ j \, {\hat\lambda }_{1j}) \; (\sum _{j} w_ j \, {\hat\lambda }_{2j}) } \]

where

\[ {\hat\lambda }_{pj} = \frac{ d_{1j} + d_{2j} }{ {\mathcal T}_{1j} + {\mathcal T}_{2j} } \]

is the combined rate estimate in stratum j under the null hypothesis of equal rates (Greenland and Robins 1985; Greenland and Rothman 2008, p. 273).

Risk Ratio Statistic

The Mantel-Haenszel risk ratio statistic is 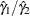${\hat\gamma }_{1} / {\hat\gamma }_{2}$, and the log ratio statistic is

\[ \mbox{log} \left( \frac{{\hat\gamma }_{1}}{{\hat\gamma }_{2}} \right) \]

Under the null hypothesis 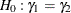$H_0: {\gamma }_{1} = {\gamma }_{2}$ (or equivalently, 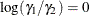$\mbox{log} ({\gamma }_{1} / {\gamma }_{2}) = 0$), the log ratio statistic has a normal distribution with mean 0 and variance

\[ V \left( \mbox{log} \left( \frac{{\hat\gamma }_{1}}{{\hat\gamma }_{2}} \right) \right) = \frac{ \sum _{j} w_ j \, ( {\hat\gamma }_{pj} - {\hat\gamma }_{1j} {\hat\gamma }_{2j} ) }{ (\sum _{j} w_ j \, {\hat\gamma }_{1j}) \; (\sum _{j} w_ j \, {\hat\gamma }_{2j}) } \]

where

\[ {\hat\gamma }_{pj} = \frac{ d_{1j} + d_{2j} }{ {\mathcal N}_{1j} + {\mathcal N}_{2j} } \]

is the combined risk estimate in stratum j under the null hypothesis of equal risks (Greenland and Robins 1985; Greenland and Rothman 2008, p. 275).