The STDRATE Procedure

Risk

Subsections:

An event risk of a population over a specified time period can be defined as the number of new events in the follow-up time period divided by the event-free population size at the beginning of the time period,

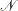\[ {\hat\gamma } = \frac{d}{\mathcal N} \]

where ${\mathcal N}$ is the population size.

For a general population, the subsets (strata) might not be homogeneous enough to have a similar risk. Thus, the risk for each stratum should be computed separately to reflect this discrepancy. For a population that consists of K homogeneous strata (such as different age groups), the stratum-specific risk for the jth stratum in a population is computed as

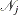\[ {\hat\gamma }_ j = \frac{d_{j}}{{\mathcal N}_{j}} \]

where ${\mathcal N}_{j}$ is the population size in the jth stratum of the population.

Assuming the number of events, 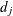$d_ j$, has a binomial distribution, then a variance estimate of 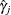${\hat\gamma }_ j$ is

\[ V( {\hat\gamma }_ j ) = \frac{ {\hat\gamma }_ j (1-{\hat\gamma }_ j) }{{\mathcal N}_ j} \]

By using the method of statistical differentials (Elandt-Johnson and Johnson 1980, pp. 70–71), the variance of the logarithm of risk can be estimated by

\[ V( \mbox{log}( {\hat\gamma }_ j ) ) = \frac{1}{ {\hat\gamma }_{j}^{2} } \, V( {\hat\gamma }_{j} ) = \frac{1}{ {\hat\gamma }_{j}^{2} } \, \frac{ {\hat\gamma _{j}} \, (1-{\hat\gamma _{j}}) }{ {\mathcal N}_{j} } = \frac{ 1-{\hat\gamma _{j}} }{ {\hat\gamma }_{j} \, {\mathcal N}_{j} } = \frac{1}{ d_{j} } - \frac{1}{ {\mathcal N}_{j} } \]

Normal Distribution Confidence Interval for Risk

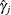A $(1-\alpha )$ confidence interval for ${\hat\gamma }_{j}$ based on a normal distribution is given by

\[ \left( \; {\hat\gamma }_{j} - z \, \sqrt {V( {\hat\gamma }_{j} )} \, , \; \; {\hat\gamma }_{j} + z \, \sqrt {V( {\hat\gamma }_{j} )} \; \right) \]

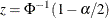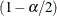where $z = \Phi ^{-1} (1-\alpha /2)$ is the $(1-\alpha /2)$ quantile of the standard normal distribution.

Lognormal Distribution Confidence Interval for Risk

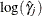A $(1-\alpha )$ confidence interval for $\mbox{log}( {\hat\gamma }_{j} )$ based on a normal distribution is given by

\[ \left( \; \mbox{log}({\hat\gamma }_{j}) - z \, \sqrt {V( \mbox{log}({\hat\gamma }_{j}) )} \, , \; \; \mbox{log}({\hat\gamma }_{j}) + z \, \sqrt {V( \mbox{log}({\hat\gamma }_{j}) )} \; \right) \]

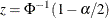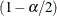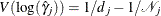where $z = \Phi ^{-1} (1-\alpha /2)$ is the $(1-\alpha /2)$ quantile of the standard normal distribution and the variance $V( \mbox{log}({\hat\gamma }_{j}) ) = 1 / d_{j} - 1 / {\mathcal N}_{j}$.

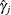Thus, a $(1-\alpha )$ confidence interval for ${\hat\gamma }_{j}$ based on a lognormal distribution is given by

\[ \left( \; {\hat\gamma }_{j} \; e^{ -z {\sqrt { \frac{1}{d_{j}} - \frac{1}{{\mathcal N}_{j}} }}} \, , \; \; {\hat\gamma }_{j} \; e^{ z {\sqrt { \frac{1}{d_{j}} - \frac{1}{{\mathcal N}_{j}} }}} \; \right) \]

Confidence Interval for Risk Difference Statistic

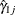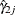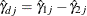For rate estimates from two independent samples, ${\hat\gamma }_{1j}$ and ${\hat\gamma }_{2j}$, a $(1-\alpha )$ confidence interval for the risk difference ${\hat\gamma }_{dj} = {\hat\gamma }_{1j} - {\hat\gamma }_{2j}$ is

\[ \left( \; {\hat\gamma }_{dj} - z \, \sqrt {V( {\hat\gamma }_{dj} )} \, , \; \; {\hat\gamma }_{dj} + z \, \sqrt {V( {\hat\gamma }_{dj} )} \; \right) \]

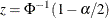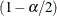where $z = \Phi ^{-1} (1-\alpha /2)$ is the $(1-\alpha /2)$ quantile of the standard normal distribution and the variance

\[ V({\hat\gamma }_{dj}) = V({\hat\gamma }_{1j}) + V({\hat\gamma }_{2j}) \]

Confidence Interval for Risk Ratio Statistic

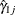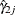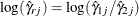For rate estimates from two independent samples, ${\hat\gamma }_{1j}$ and ${\hat\gamma }_{2j}$, a $(1-\alpha )$ confidence interval for the log risk ratio statistic $\mbox{log} ({\hat\gamma }_{rj}) = \mbox{log} ({\hat\gamma }_{1j} / {\hat\gamma }_{2j})$ is

\[ \left( \; \mbox{log} ({\hat\gamma }_{rj}) - z \, \sqrt {V( \mbox{log} ({\hat\gamma }_{rj}) )} \, , \; \; \mbox{log} ({\hat\gamma }_{rj}) + z \, \sqrt {V( \mbox{log} ({\hat\gamma }_{rj}) )} \; \right) \]

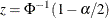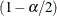where $z = \Phi ^{-1} (1-\alpha /2)$ is the $(1-\alpha /2)$ quantile of the standard normal distribution and the variance

\[ V( \mbox{log} ({\hat\gamma }_{rj}) = V( \mbox{log} ({\hat\gamma }_{1j}) ) + V( \mbox{log} ({\hat\gamma }_{2j}) ) \]

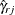Thus, a $(1-\alpha )$ confidence interval for the risk ratio statistic ${\hat\gamma }_{rj}$ is given by

\[ \left( \; \frac{{\hat\gamma }_{1j}}{{\hat\gamma }_{2j}} \; e^{ -z \sqrt {V( \mbox{log} ({\hat\gamma }_{rj}) ) } } \, , \; \; \frac{{\hat\gamma }_{1j}}{{\hat\gamma }_{2j}} \; e^{ z \sqrt {V( \mbox{log} ({\hat\gamma }_{rj}) ) } } \; \right) \]

Confidence Interval for Risk SMR

At stratum j, a stratum-specific standardized morbidity/mortality ratio is

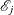\[ {\mathcal R}_{j} = \; \frac{\, d_ j \, }{{\mathcal E}_ j} \]

where ${\mathcal E}_ j$ is the expected number of events.

With the risk

\[ {\hat\gamma }_ j = \frac{d_{j}}{{\mathcal N}_{j}} \]

SMR can be expressed as

\[ {\mathcal R}_{j} = \; \frac{\, {\mathcal N}_ j \, }{{\mathcal E}_ j} \; {\hat\gamma }_ j \]

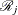Thus, a $(1-\alpha )$ confidence interval for ${\mathcal R}_ j$ is given by

\[ \left( \; \frac{\, {\mathcal N}_ j \, }{{\mathcal E}_ j} \; {\hat\gamma }_{jl} \, , \; \; \frac{\, {\mathcal N}_ j \, }{{\mathcal E}_ j} \; {\hat\gamma }_{ju} \; \right) \]

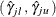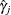where $(\, {\hat\gamma }_{jl} \, , \, {\hat\gamma }_{ju} \, )$ is a $(1-\alpha )$ confidence interval for the risk ${\hat\gamma }_ j$.