The NPAR1WAY Procedure
Stratified Analysis
PROC NPAR1WAY provides stratified analysis of two-sample data for the following score types: Wilcoxon, median, Van der Waerden (normal), Savage, and data scores. It computes the stratified test statistic by combining the stratum-level linear rank statistics for the score type that you specify. The section Scores for Linear Rank and One-Way ANOVA Tests describes the computation of the rank-based scores. For stratified analysis, you can compute the scores by using within-stratum ranks or overall ranks. By default, or if you specify the RANKS=STRATUM option, PROC NPAR1WAY ranks and scores the response values separately within each stratum. If you specify the RANKS=OVERALL option, PROC NPAR1WAY ranks and scores the response values overall (without regard to stratum classification). For more information, see Mehrotra, Lu, and Li (2010), Lehmann and D’Abrera (2006), and Van Elteren (1960).
The stratified rank sum statistic T is computed as
![\[ T = \sum _{k=1}^ K S_ k / w_ k \]](images/statug_npar1way0050.png)
where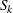 
is the sum of the rank-based scores for stratum k (as described in the section Simple Linear Rank Tests for Two-Sample Data), 
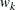is the weight of stratum k, and K is the total number of strata. By default, or if you specify the WEIGHTS=STRATUM
option, PROC NPAR1WAY computes the stratum weights as 
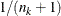, where 
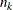is the number of observations in stratum k. If you specify the WEIGHTS=EQUAL
option, the stratum weight (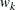) is 1 for all strata.
The expected value and variance of T are similarly computed by combining stratum-level values as
![\[ \mr{E_0}(T) = \sum _{k=1}^ K \mr{E_0}(S_ k) / w_ k \]](images/statug_npar1way0055.png)
![\[ \mr{Var_0}(T) = \sum _{k=1}^ K \mr{Var_0}(S_ k) / w_ k^2 \]](images/statug_npar1way0056.png)
where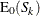 
and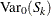 
are the expected value and variance of the rank sum statistic for stratum k. For more information, see the section Simple Linear Rank Tests for Two-Sample Data.
The stratified test statistic is computed as
![\[ z = \left( T - \mr{E_0}(T) \right) / \sqrt { \mr{Var_0}(T) } \]](images/statug_npar1way0059.png)
Under the null hypothesis of no difference between the two classification levels, the test statistic has a standard normal distribution. PROC NPAR1WAY provides one-sided and two-sided asymptotic p-values for the test as described in the section Definition of p-Values.
PROC NPAR1WAY defines the reference class group (sample) for the stratified two-sample analysis by considering the number of observations (total frequency) across all strata. The reference group is defined as the smaller of the two samples. If both samples have the same number of observations, the reference group is defined as the level that appears first in the input data set. Each stratum rank sum statistic is then computed as the sum of the scores for the observations in the reference group. PROC NPAR1WAY lists the reference group first in the "Class Information" table.