The LIFEREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesModel SpecificationComputational MethodSupported DistributionsPredicted ValuesConfidence IntervalsFit StatisticsProbability PlottingINEST= Data SetOUTEST= Data SetXDATA= Data SetComputational ResourcesBayesian AnalysisDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisODS Table NamesODS Graphics
Missing ValuesModel SpecificationComputational MethodSupported DistributionsPredicted ValuesConfidence IntervalsFit StatisticsProbability PlottingINEST= Data SetOUTEST= Data SetXDATA= Data SetComputational ResourcesBayesian AnalysisDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisODS Table NamesODS Graphics -
Examples
 Motorette FailureComputing Predicted Values for a Tobit ModelOvercoming Convergence Problems by Specifying Initial ValuesAnalysis of Arbitrarily Censored Data with Interaction EffectsProbability Plotting—Right CensoringProbability Plotting—Arbitrary CensoringBayesian Analysis of Clinical Trial DataModel Postfitting Analysis
Motorette FailureComputing Predicted Values for a Tobit ModelOvercoming Convergence Problems by Specifying Initial ValuesAnalysis of Arbitrarily Censored Data with Interaction EffectsProbability Plotting—Right CensoringProbability Plotting—Arbitrary CensoringBayesian Analysis of Clinical Trial DataModel Postfitting Analysis - References
Confidence Intervals
Confidence intervals are computed for all model parameters and are reported in the "Analysis of Parameter Estimates" table.
The confidence coefficient can be specified with the ALPHA= MODEL statement option, resulting in a
MODEL statement option, resulting in a 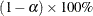 two-sided confidence coefficient. The default confidence coefficient is 95%, corresponding to
two-sided confidence coefficient. The default confidence coefficient is 95%, corresponding to  .
.
Regression Parameters
A two-sided 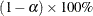 confidence interval
confidence interval ![$[\beta _{iL},\; \; \beta _{iU}]$](images/statug_lifereg0173.png) for the regression parameter
for the regression parameter  is based on the asymptotic normality of the maximum likelihood estimator
is based on the asymptotic normality of the maximum likelihood estimator  and is computed by
and is computed by
![\[ \beta _{iL}=\hat{\beta }_{i} - z_{1-\alpha /2}(\mr{SE}_{\hat{\beta }_{i}}) \]](images/statug_lifereg0176.png)
![\[ \beta _{iU}=\hat{\beta }_{i} + z_{1-\alpha /2}(\mr{SE}_{\hat{\beta }_{i}}) \]](images/statug_lifereg0177.png)
where  is the estimated standard error of
is the estimated standard error of  , and
, and 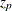 is the
is the 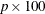 percentile of the standard normal distribution.
percentile of the standard normal distribution.
Scale Parameter
A two-sided 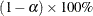 confidence interval
confidence interval ![$[\sigma _ L,\; \; \sigma _ U]$](images/statug_lifereg0181.png) for the scale parameter
for the scale parameter  in the location-scale model is based on the asymptotic normality of the logarithm of the maximum likelihood estimator
in the location-scale model is based on the asymptotic normality of the logarithm of the maximum likelihood estimator  , and is computed by
, and is computed by
![\[ \sigma _{L}=\hat{\sigma }/\exp [z_{1-\alpha /2}\mr{(SE}_{\hat{\sigma }})/\hat{\sigma }] \]](images/statug_lifereg0183.png)
![\[ \sigma _{U}=\hat{\sigma }\exp [z_{1-\alpha /2}\mr{(SE}_{\hat{\sigma }})/\hat{\sigma }] \]](images/statug_lifereg0184.png)
See Meeker and Escobar (1998) for more information.
Weibull Scale and Shape Parameters
The Weibull distribution scale parameter  and shape parameter
and shape parameter  are obtained by transforming the extreme-value location parameter
are obtained by transforming the extreme-value location parameter 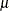 and scale parameter
and scale parameter  :
:
![\[ \eta = \exp (\mu ) \]](images/statug_lifereg0187.png)
![\[ \beta = 1 / \sigma \]](images/statug_lifereg0188.png)
Consequently, two-sided 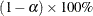 confidence intervals for the Weibull scale and shape parameters are computed as
confidence intervals for the Weibull scale and shape parameters are computed as
![\[ [\eta _ L,\; \; \eta _ U ] = [\exp (\mu _ L),\; \; \exp (\mu _ U)] \]](images/statug_lifereg0189.png)
![\[ [\beta _ L,\; \; \beta _ U] = [1/\sigma _ U,\; \; 1/\sigma _ L] \]](images/statug_lifereg0190.png)
Gamma Shape Parameter
A two-sided 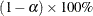 confidence interval for the three-parameter gamma shape parameter
confidence interval for the three-parameter gamma shape parameter 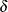 is computed by
is computed by
![\[ [\delta _ L,\; \; \delta _ U] = [ \hat{\delta } - z_{1-\alpha /2}(\mr{SE}_{\hat{\delta }}), \; \; \hat{\delta } + z_{1-\alpha /2}(\mr{SE}_{\hat{\delta }}) ] \]](images/statug_lifereg0191.png)