The HPNLMOD Procedure

Least Squares Model

The Michaelis-Menten model of enzyme kinetics (Ratkowsky 1990, p. 59) relates a substrate’s concentration to its catalyzed reaction rate. The Michaelis-Menten model can be analyzed using a least squares estimation because it does not specify how the reaction rate is distributed around its predicted value. The relationship between reaction rate and substrate concentration is

\[ f(\mb{x}, \btheta ) = \frac{\theta _1 x_ i}{\theta _2 + x_ i}, \quad \mbox{for} \, \, i = 1, 2, \ldots , n \]

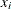where $x_ i$ represents the concentration for n trials and 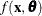$f(\mb{x}, \btheta )$ is the reaction rate. The vector 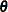$\btheta $ contains the rate parameters.

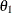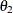For this model, which has experimental measurements of reaction rate and concentration stored in the enzyme data set, the following SAS statements estimate the parameters $\theta _1$ and $\theta _2$: 

proc hpnlmod data=enzyme;
   parms theta1=0 theta2=0;
   model rate ~ residual(theta1*conc / (theta2 + conc));
run;

The least squares estimation performed by PROC HPNLMOD for this enzyme kinetics problem produces the analysis of variance table that is displayed in Figure 56.1. The table displays the degrees of freedom, sums of squares, and mean squares along with the model F test.

Figure 56.1: Nonlinear Least Squares Analysis of Variance

The HPNLMOD Procedure

Analysis of Variance
Source DF Sum of Squares Mean Square F Value Approx
Pr > F
Model 2 290116 145058 88537.2 <.0001
Error 12 19.6606 1.6384    
Uncorrected Total 14 290135      

An intercept was not specified for this model. 





            

            


            
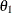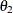Finally, Figure 56.2 displays the parameter estimates, standard errors, t statistics, and 95% confidence intervals for $\theta _1$ and $\theta _2$. 
            

            
  

            

               
Figure 56.2:  Parameter Estimates and Approximate 95% Confidence Intervals

               

                  

                     
                     

                        
                        
                        

                           
                           

                              
                              














Parameter Estimates
                                       
                                    



Parameter
                                       
                                       Estimate
                                       
                                       Standard
Error
                                       		
                                       
                                       DF
                                       
                                       t Value
                                       
                                       Approx
Pr > |t|
                                       		
                                       
                                       Approximate 95% Confidence
Limits
                                       		
                                       
                                    





theta1
                                       
                                       158.1
                                       
                                       0.6737
                                       
                                       1
                                       
                                       234.67
                                       
                                       <.0001
                                       
                                       156.6
                                       
                                       159.6
                                       
                                    



theta2
                                       
                                       0.0741
                                       
                                       0.00313
                                       
                                       1
                                       
                                       23.69
                                       
                                       <.0001
                                       
                                       0.0673
                                       
                                       0.0809
                                       
                                    






                           
                        

                        



                     
                     
                  





            

            


            
In the enzyme kinetics model, no information was supplied about the distribution of the reaction rate around the model’s mean
               value. Therefore, the residual model distribution was specified to perform a least squares parameter fit.