The HPMIXED Procedure
Computational Approach
The computational methods to efficiently solve large mixed model problems with the HPMIXED procedure rely on a combination of several techniques, including sparse matrix storage, specialized solving of sparse linear systems, and dedicated nonlinear optimization.
Sparse Storage and Computation
One of the fundamental computational tasks in analyzing a linear mixed model is solving the mixed model equations
![\[ \left[ \begin{array}{cc} \bX ’\bX & \bX ’\bZ \\ \bZ ’\bX & \bZ ’\bZ + \sigma ^2 \bG ^{-1} \end{array}\right] \left[\begin{array}{c} \bbeta \\ \bgamma \end{array}\right] = \left[\begin{array}{c} \bX ’\mb{y} \\ \bZ ’\mb{y} \end{array}\right] \]](images/statug_hpmixed0013.png)
where 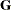 denotes the variance matrix of the random effects. The mixed model crossproduct matrix
denotes the variance matrix of the random effects. The mixed model crossproduct matrix
![\[ \left[ \begin{array}{cc} \bX ’\bX & \bX ’\bZ \\ \bZ ’\bX & \bZ ’\bZ + \sigma ^2 \bG ^{-1} \end{array}\right] \]](images/statug_hpmixed0015.png)
is a key component of these equations, and it often has many zero values (George and Liu 1981). Sparse storage techniques can result in significant savings in both memory and CPU resources. The HPMIXED procedure draws on sparse matrix representation and storage where appropriate or necessary.
Conjugate Gradient Algorithm and Iteration-on-Data Technology
Solving the mixed model equations is a critical component of linear mixed model analysis. The two main components of the preconditioned
conjugate gradient (PCCG) algorithm are preconditioning and matrix-vector product computing (Shewchuk 1994). The algorithm is guaranteed to converge to the solution within  iterations, where
iterations, where  is equal to the number of distinct eigenvalues of the mixed model equations. This simple yet powerful algorithm can be easily
implemented with an iteration-on-data (IOD) technique (Tsuruta, Misztal, and Stranden 2001) that can yield significant savings of memory resources.
is equal to the number of distinct eigenvalues of the mixed model equations. This simple yet powerful algorithm can be easily
implemented with an iteration-on-data (IOD) technique (Tsuruta, Misztal, and Stranden 2001) that can yield significant savings of memory resources.
The combination of the PCCG algorithm and iteration on data makes it possible to efficiently compute best linear unbiased predictors (BLUPs) for the random effects in mixed models with large mixed model equations.
Average Information Algorithm
The HPMIXED procedure estimates covariance parameters by restricted maximum likelihood. The default optimization method is a quasi-Newton algorithm. When the Hessian or information matrix is required, the HPMIXED procedure takes advantage of the computational simplifications that are available by averaging information (AI). The AI algorithm (Johnson and Thompson 1995; Gilmour, Thompson, and Cullis 1995) replaces the second derivative matrix with the average of the observed and expected information matrices. The computationally intensive trace terms in these information matrices cancel upon averaging. Coarsely, the AI algorithm can be viewed as a hybrid of a Newton-Raphson approach and Fisher scoring.
