The HPMIXED Procedure

Computing Starting Values by EM-REML

The EM-REML algorithm (Dempster, Laird, and Rubin 1977) iteratively alternates between an expectation step and a maximization step to maximize the restricted log likelihood. The algorithm is based on augmenting the observed data 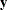$\mb{y}$ with the unobservable random effects 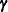$\bgamma $, leading to a simplified form for the log likelihood. For example, if 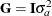$\bG =\bI \sigma ^2_ a$ then given the realized values 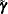$\tilde{\bgamma }$ of the unobservable random effects 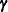$\bgamma $, the REML estimate of 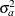$\sigma ^2_ a$ satisfies

\[ \widehat{\sigma }^2_ a = \frac{\tilde{\bgamma }'\tilde{\bgamma }}{q - \sigma ^2/\sigma ^2_ a\mbox{tr}(\bC ^{aa})} \]

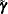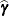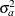This corresponds to the maximization step of EM-REML. However, the true realized values $\tilde{\bgamma }$ are unknown in practice. The expectation step of EM-REML replaces them with the conditional expected values $\widehat{\bgamma }$ of the random effects, given the observed data $\mb{y}$ and initial values for the parameters. The new estimate of $\sigma ^2_ a$ is used in turn to recalculate the conditional expected values, and the iteration is repeated until convergence.

It is well known that EM-REML is generally more robust against a poor choice of starting values than general nonlinear optimization methods such as Newton-Raphson, though it tends to converge slowly as it approaches the optimum. The Newton-Raphson method, on the other hand, converges much faster when it has a good set of starting values. The HPMIXED procedure, thus, employs a scheme that uses EM-REML initially in order to get good starting values, and after a few iterations, when the decrease in log likelihood has significantly slowed down, switching to a more general nonlinear optimization technique (by default, quasi-Newton).