The HPLMIXED Procedure
Estimating Fixed and Random Effects in the Mixed Model
ML and REML methods provide estimates of 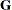 and
and 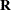 , which are denoted
, which are denoted 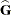 and
and 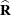 , respectively. To obtain estimates of
, respectively. To obtain estimates of 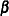 and predicted values of
and predicted values of 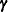 , the standard method is to solve the mixed model equations (Henderson 1984):
, the standard method is to solve the mixed model equations (Henderson 1984):
![\[ \left[\begin{array}{lr} \bX ’\widehat{\bR }^{-1}\bX & \bX ’\widehat{\bR }^{-1}\bZ \\*\bZ ’\widehat{\bR }^{-1}\bX & \bZ ’\widehat{\bR }^{-1}\bZ + \widehat{\bG }^{-1} \end{array}\right] \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\bgamma } \end{array} \right] = \left[\begin{array}{r} \bX ’\widehat{\bR }^{-1}\mb{y} \\ \bZ ’\widehat{\bR }^{-1}\mb{y} \end{array} \right] \]](images/statug_hplmixed0191.png)
The solutions can also be written as
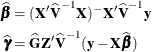
and have connections with empirical Bayes estimators (Laird and Ware 1982; Carlin and Louis 1996). Note that the 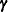 are random variables and not parameters (unknown constants) in the model. Technically, determining values for
are random variables and not parameters (unknown constants) in the model. Technically, determining values for 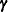 from the data is thus a prediction task, whereas determining values for
from the data is thus a prediction task, whereas determining values for 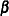 is an estimation task.
is an estimation task.
The mixed model equations are extended normal equations. The preceding expression assumes that 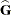 is nonsingular. For the extreme case where the eigenvalues of
is nonsingular. For the extreme case where the eigenvalues of 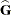 are very large,
are very large, 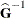 contributes very little to the equations and
contributes very little to the equations and 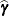 is close to what it would be if
is close to what it would be if 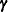 actually contained fixed-effects parameters. On the other hand, when the eigenvalues of
actually contained fixed-effects parameters. On the other hand, when the eigenvalues of 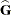 are very small,
are very small, 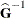 dominates the equations and
dominates the equations and 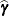 is close to 0. For intermediate cases,
is close to 0. For intermediate cases, 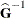 can be viewed as shrinking the fixed-effects estimates of
can be viewed as shrinking the fixed-effects estimates of 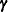 toward 0 (Robinson 1991).
toward 0 (Robinson 1991).
If 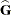 is singular, then the mixed model equations are modified (Henderson 1984) as follows:
is singular, then the mixed model equations are modified (Henderson 1984) as follows:
![\[ \left[\begin{array}{lr} \bX ’\widehat{\bR } ^{-1}\bX & \bX ’\widehat{\bR } ^{-1} \bZ \widehat{\bG } \\ \widehat{\bG }’\bZ ’\widehat{\bR } ^{-1}\bX & \widehat{\bG }’\bZ ’\widehat{\bR } ^{-1}\bZ \widehat{\bG } + \bG \end{array}\right] \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\btau } \end{array} \right] = \left[\begin{array}{r} \bX ’\widehat{\bR } ^{-1}\mb{y} \\ \widehat{\bG }’\bZ ’\widehat{\bR } ^{-1}\mb{y} \end{array} \right] \]](images/statug_hplmixed0194.png)
Denote the generalized inverses of the nonsingular 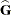 and singular
and singular 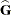 forms of the mixed model equations by
forms of the mixed model equations by 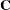 and
and 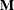 , respectively. In the nonsingular case, the solution
, respectively. In the nonsingular case, the solution 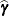 estimates the random effects directly. But in the singular case, the estimates of random effects are achieved through a back-transformation
estimates the random effects directly. But in the singular case, the estimates of random effects are achieved through a back-transformation
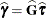 where
where 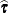 is the solution to the modified mixed model equations. Similarly, while in the nonsingular case
is the solution to the modified mixed model equations. Similarly, while in the nonsingular case 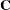 itself is the estimated covariance matrix for
itself is the estimated covariance matrix for 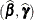 , in the singular case the covariance estimate for
, in the singular case the covariance estimate for 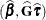 is given by
is given by 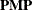 where
where
![\[ \bP = \left[\begin{array}{cc} \bI & \\ & \widehat{\bG } \end{array}\right] \]](images/statug_hplmixed0202.png)
An example of when the singular form of the equations is necessary is when a variance component estimate falls on the boundary constraint of 0.
