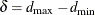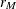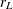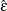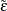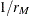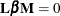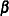The GLMPOWER Procedure
POWER Statement
-
POWER <options>;
The POWER statement performs power and sample size analyses for the Type III F tests that are specified in the MTEST= option, for each effect in the model that is defined by the MODEL statement, and for the contrasts that are defined by all CONTRAST , MANOVA , and REPEATED statements. The POWER statement must appear after the MODEL statement if the EFFECTS= option is used in the POWER statement.
For information about the power and sample size computational methods and formulas, see the section Computational Methods and Formulas.
Summary of Options
Table 48.5 summarizes the options available in the POWER statement.
Table 48.5: POWER Statement Options
|
Option |
Description |
|---|---|
|
Specify test statistic |
|
|
Specifies the test statistic for a multivariate model |
|
|
Specifies the form of the Huynh-Feldt epsilon for MTEST=HF |
|
|
Specify analysis information |
|
|
Specifies the level of significance of each test |
|
|
Specifies the model effects |
|
|
Specify covariates for a univariate model |
|
|
Specifies multiple correlation ( |
|
|
Specifies additional degrees of freedom due to covariates |
|
|
Specifies proportional variance reduction (r) due to covariates |
|
|
Specify variability |
|
|
Specifies the correlation matrix of the dependent variables in a multivariate model |
|
|
Specifies the correlations among the dependent variables in a multivariate model |
|
|
Specifies the covariance matrix of the dependent variables in a multivariate model |
|
|
Defines a matrix or vector |
|
|
Specifies the vector of error standard deviations for each dependent variable in a multivariate model |
|
|
Specifies the common error standard deviation |
|
|
Specify sample size |
|
|
Enables fractional input and output for sample sizes |
|
|
Specifies the sample size |
|
|
Specify power |
|
|
Specifies power |
|
|
Choose computational method |
|
|
Specifies the computational method for multivariate tests |
|
|
Control ordering in output |
|
|
Specifies the location of the Dependent or Transformation column in the output |
|
|
Controls ordering in output |
|
Table 48.6 summarizes the valid result parameters.
Table 48.6: Summary of Result Parameters in the POWER Statement
|
Solve for |
Syntax |
|---|---|
|
Power |
POWER = . |
|
Sample size |
NTOTAL = . |
Dictionary of Options
Restrictions on Option Combinations
To specify the variability in a multivariate model, choose one of the following parameterizations:
-
standard deviations and correlations (using the MATRIX= , SQRTVAR= , and CORRS= options)
-
common standard deviation and correlations (using the STDDEV= , MATRIX= , and CORRS= options)
-
standard deviations and correlation matrix (using the MATRIX= , SQRTVAR= , and CORRMAT= options)
-
common standard deviation and correlation matrix (using the STDDEV= , MATRIX= , and CORRMAT= options)
For the relationship between covariates and response in a univariate model, specify either the multiple correlation (by using the CORRXY= option) or the proportional reduction in total R square (by using the PROPVARREDUCTION= option).

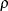

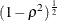
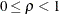
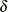
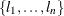
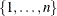
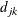
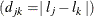
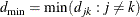
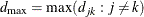
![\begin{equation*} \rho _{jk} = \begin{cases} 1 & \text {if \Mathtext{j} = \Mathtext{k}}\\ \rho ^{d_\mr {min} + \delta [(d_{jk}-d_\mr {min})/(d_\mr {max}-d_\mr {min})]} & \text {if $j \ne k$ and $d_\mr {min} \ne d_\mr {max}$}\\ \rho & \text {if $j \ne k$ and $d_\mr {min}=d_\mr {max}$} \end{cases}\end{equation*}](images/statug_glmpower0031.png)