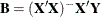The GLMPOWER Procedure
CONTRAST Statement
-
CONTRAST ’label’ effect values <…effect values> </ options>;
The CONTRAST
statement enables you to define custom Type III hypothesis tests by specifying an  vector or matrix for testing either the hypothesis
vector or matrix for testing either the hypothesis 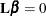 (for univariate models) or the hypothesis
(for univariate models) or the hypothesis 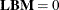 (for multivariate models). The
(for multivariate models). The  matrix consists of one or more between-subject contrasts.
matrix consists of one or more between-subject contrasts.
To use this feature, you must be familiar with the details of the model parameterization that PROC GLM uses. For more information,
see the section Parameterization of PROC GLM Models in Chapter 46: The GLM Procedure. All the elements of the  matrix can be given, or if only certain portions of the
matrix can be given, or if only certain portions of the  matrix are given, PROC GLMPOWER constructs the remaining elements from the context (in a manner similar to that in rule 4
in the section Construction of Least Squares Means in Chapter 46: The GLM Procedure).
matrix are given, PROC GLMPOWER constructs the remaining elements from the context (in a manner similar to that in rule 4
in the section Construction of Least Squares Means in Chapter 46: The GLM Procedure).
There is no limit to the number of CONTRAST statements that you can specify, but they must appear after the MODEL statement. Each power analysis includes tests for all CONTRAST statements.
You can specify the following arguments:
- label
-
identifies the contrast in the output. A label is required for every contrast that is specified. Labels must be enclosed in single or double quotation marks.
- effect
-
identifies an effect that appears in the MODEL statement, or the INTERCEPT effect. You do not need to include all effects that appear in the MODEL statement.
- values
-
are constants that are elements of the
 matrix associated with the effect.
matrix associated with the effect.
You can specify the following option in the CONTRAST statement after a slash (/):

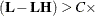
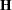
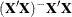
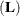
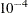
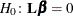
![\[ (\mb{Lb})^{\prime }(\mb{L}(\mb{X^{\prime }X})^{-} \mb{L}^{\prime })^{-1}(\mb{Lb}) \]](images/statug_glmpower0011.png)
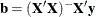
![\[ \mb{H} = \mb{M}’(\mb{LB})’ (\mb{L}(\mb{X'X})^{-} \mb{L}’)^{-1} (\mb{LB})\mb{M} \]](images/statug_glmpower0013.png)