The GLMPOWER Procedure
Adjustments for Covariates in Univariate Models
If you specify covariates in a univariate model (whether continuous or categorical), then two adjustments are made in order
to compute approximate power in the presence of the covariates. Let 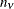 denote the number of covariates (counting dummy variables for categorical covariates individually) as specified in the NCOVARIATES=
option in the POWER
statement. In other words,
denote the number of covariates (counting dummy variables for categorical covariates individually) as specified in the NCOVARIATES=
option in the POWER
statement. In other words, 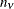 is the total degrees of freedom used by the covariates. The adjustments are as follows:
is the total degrees of freedom used by the covariates. The adjustments are as follows:
-
The error degrees of freedom decrease by
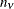 .
.
-
The error standard deviation
 shrinks by a factor of
shrinks by a factor of 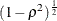 (if the CORRXY=
option is used to specify the correlation
(if the CORRXY=
option is used to specify the correlation 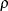 between covariates and response) or
between covariates and response) or 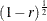 (if the PROPVARREDUCTION=
option is used to specify the proportional reduction in total
(if the PROPVARREDUCTION=
option is used to specify the proportional reduction in total 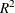 incurred by the covariates). Let
incurred by the covariates). Let  represent the updated value of
represent the updated value of  .
.
As a result of these changes, the power is computed as
![\[ \mr{power} = P\left(F(r_ L, \mr{DF_ E}-n_\nu , \lambda ^\star ) \ge F_{1-\alpha }(r_ L, N-r_ x-n_\nu )\right) \]](images/statug_glmpower0079.png)
where 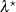 is calculated using
is calculated using  rather than
rather than  :
:
![\[ \lambda ^\star = N \left(\mb{L} \bbeta - \btheta _0 \right)’\left(\mb{L} \left(\ddot{\mb{X}}’ \mb{W} \ddot{\mb{X}} \right)^{-1} \mb{L}^\prime \right)^{-1} \left(\mb{L} \bbeta - \btheta _0 \right) (\sigma ^\star )^{-2} \]](images/statug_glmpower0081.png)
