The GLMPOWER Procedure
Contrasts in Fixed-Effect Univariate Models
The univariate linear model has the form
![\[ \mb{y} = \mb{X} \bbeta + \bepsilon \]](images/statug_glmpower0042.png)
where 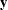 is the N
is the N  1 vector of responses,
1 vector of responses, 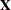 is the N
is the N  k design matrix,
k design matrix, 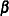 is the k
is the k  1 vector of model parameters that correspond to the columns of
1 vector of model parameters that correspond to the columns of 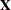 , and
, and  is an N
is an N  1 vector of errors with
1 vector of errors with
![\[ \epsilon _1, \ldots , \epsilon _ N \sim \mr{N}(0,\sigma ^2) \quad \mr{(iid)} \]](images/statug_glmpower0046.png)
In PROC GLMPOWER, the model parameters 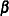 are not specified directly, but rather indirectly as
are not specified directly, but rather indirectly as 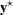 , which represents either conjectured response means or typical response values for each design profile. The
, which represents either conjectured response means or typical response values for each design profile. The 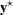 values are manifested as the dependent variable in the MODEL
statement. The vector
values are manifested as the dependent variable in the MODEL
statement. The vector 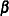 is obtained from
is obtained from 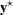 according to the least squares equation,
according to the least squares equation,
![\[ \bbeta = (\mb{X}’\mb{X})^{-}\mb{X}’ \mb{y^\star } \]](images/statug_glmpower0048.png)
Note that, in general, there is not a one-to-one mapping between 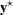 and
and 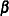 . Many different scenarios for
. Many different scenarios for 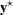 might lead to the same
might lead to the same 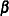 . If you specify
. If you specify 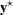 with the intention of representing cell means, keep in mind that PROC GLMPOWER allows scenarios that are not valid cell means according to the model that is specified in the MODEL
statement. For example, if
with the intention of representing cell means, keep in mind that PROC GLMPOWER allows scenarios that are not valid cell means according to the model that is specified in the MODEL
statement. For example, if 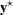 exhibits an interaction effect but the corresponding interaction term is left out of the model, then the cell means (
exhibits an interaction effect but the corresponding interaction term is left out of the model, then the cell means (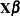 ) that are derived from
) that are derived from 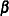 differ from
differ from 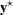 . In particular, the cell means that are derived in this way are the projection of
. In particular, the cell means that are derived in this way are the projection of 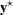 onto the model space.
onto the model space.
It is convenient in power analysis to parameterize the design matrix 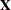 in three parts,
in three parts, 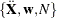 , defined as follows:
, defined as follows:
-
The q
 k essence design matrix
k essence design matrix 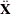 is the collection of unique rows of
is the collection of unique rows of 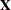 . Its rows are sometimes referred to as "design profiles." Here, q
. Its rows are sometimes referred to as "design profiles." Here, q 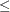 N is defined simply as the number of unique rows of
N is defined simply as the number of unique rows of 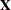 .
.
-
The q
 1 weight vector
1 weight vector 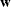 reveals the relative proportions of design profiles, and
reveals the relative proportions of design profiles, and 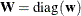 . Row i of
. Row i of 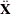 is to be included in the design
is to be included in the design 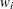 times for every
times for every 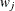 times that row j is included. The weights are assumed to be standardized (that is, they sum up to 1).
times that row j is included. The weights are assumed to be standardized (that is, they sum up to 1).
-
The total sample size is N. This is the number of rows in
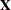 . If you gather
. If you gather 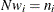 copies of the ith row of
copies of the ith row of 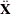 , for
, for 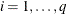 , then you end up with
, then you end up with 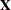 .
.
The preceding quantities are derived from PROC GLMPOWER syntax as follows:
It is useful to express the crossproduct matrix 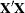 in terms of these three parts,
in terms of these three parts,
![\[ \mb{X}’\mb{X} = N \ddot{\mb{X}}’ \mb{W} \ddot{\mb{X}} \]](images/statug_glmpower0060.png)
because this expression factors out the portion (N) that depends on sample size and the portion (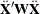 ) that depends only on the design structure.
) that depends only on the design structure.
A general linear hypothesis for the univariate model has the form
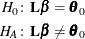
where  is an l
is an l  k contrast matrix with rank
k contrast matrix with rank 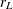 and
and 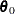 is the null value (usually just a vector of zeros).
is the null value (usually just a vector of zeros).
Note that model effect tests are just contrasts that use special forms of  . Thus, this scheme covers both effect tests (which are specified in the MODEL
statement and the EFFECTS=
option in the POWER
statement) and custom contrasts (which are specified in the CONTRAST
statement).
. Thus, this scheme covers both effect tests (which are specified in the MODEL
statement and the EFFECTS=
option in the POWER
statement) and custom contrasts (which are specified in the CONTRAST
statement).
The model degrees of freedom 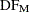 are equal to the rank of
are equal to the rank of 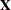 , denoted
, denoted 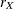 . The error degrees of freedom
. The error degrees of freedom 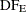 are equal to N –
are equal to N – 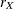 . The sample size N must be at least
. The sample size N must be at least 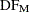 plus the number of covariates.
plus the number of covariates.
The test statistic is
![\[ F = \frac{\left(\frac{\mr{SS_ H}}{r_ L}\right)}{\hat{\sigma }^2} \]](images/statug_glmpower0067.png)
where
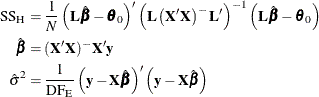
Under 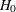 ,
, 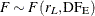 . Under
. Under 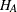 , F is distributed as
, F is distributed as 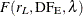 with noncentrality
with noncentrality
![\[ \lambda = N \left(\mb{L} \bbeta - \btheta _0 \right)’\left(\mb{L} \left(\ddot{\mb{X}}’ \mb{W} \ddot{\mb{X}} \right)^{-1} \mb{L}^\prime \right)^{-1} \left(\mb{L} \bbeta - \btheta _0 \right) \sigma ^{-2} \]](images/statug_glmpower0073.png)
The value of  is specified in the STDDEV=
option in the POWER
statement.
is specified in the STDDEV=
option in the POWER
statement.
Muller and Peterson (1984) give the exact power of the test as
![\[ \mr{power} = P\left(F(r_ L, \mr{DF_ E}, \lambda ) \ge F_{1-\alpha }(r_ L, \mr{DF_ E})\right) \]](images/statug_glmpower0075.png)
The value of  is specified in the ALPHA=
option in the POWER
statement.
is specified in the ALPHA=
option in the POWER
statement.
Sample size is computed by inverting the power equation.
See Muller and Benignus (1992) and O’Brien and Shieh (1992) for additional discussion.
