The TRANSREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Model Statement UsageBox-Cox TransformationsUsing Splines and KnotsScoring Spline VariablesLinear and Nonlinear Regression FunctionsSimultaneously Fitting Two Regression FunctionsPenalized B-SplinesSmoothing SplinesSmoothing Splines Changes and EnhancementsIteration History Changes and EnhancementsANOVA CodingsMissing ValuesMissing Values, UNTIE, and Hypothesis TestsControlling the Number of IterationsUsing the REITERATE Algorithm OptionAvoiding Constant TransformationsConstant VariablesCharacter OPSCORE VariablesConvergence and DegeneraciesImplicit and Explicit InterceptsPassive ObservationsPoint ModelsRedundancy AnalysisOptimal ScalingOPSCORE, MONOTONE, UNTIE, and LINEAR TransformationsSPLINE and MSPLINE TransformationsSpecifying the Number of KnotsSPLINE, BSPLINE, and PSPLINE ComparisonsHypothesis TestsOutput Data SetOUTTEST= Output Data SetComputational ResourcesUnbalanced ANOVA without CLASS VariablesHypothesis Tests for Simple Univariate ModelsHypothesis Tests with Monotonicity ConstraintsHypothesis Tests with Dependent Variable TransformationsHypothesis Tests with One-Way ANOVAUsing the DESIGN Output OptionDiscrete Choice Experiments: DESIGN, NORESTORE, NOZEROCenteringDisplayed OutputODS Table NamesODS Graphics
Model Statement UsageBox-Cox TransformationsUsing Splines and KnotsScoring Spline VariablesLinear and Nonlinear Regression FunctionsSimultaneously Fitting Two Regression FunctionsPenalized B-SplinesSmoothing SplinesSmoothing Splines Changes and EnhancementsIteration History Changes and EnhancementsANOVA CodingsMissing ValuesMissing Values, UNTIE, and Hypothesis TestsControlling the Number of IterationsUsing the REITERATE Algorithm OptionAvoiding Constant TransformationsConstant VariablesCharacter OPSCORE VariablesConvergence and DegeneraciesImplicit and Explicit InterceptsPassive ObservationsPoint ModelsRedundancy AnalysisOptimal ScalingOPSCORE, MONOTONE, UNTIE, and LINEAR TransformationsSPLINE and MSPLINE TransformationsSpecifying the Number of KnotsSPLINE, BSPLINE, and PSPLINE ComparisonsHypothesis TestsOutput Data SetOUTTEST= Output Data SetComputational ResourcesUnbalanced ANOVA without CLASS VariablesHypothesis Tests for Simple Univariate ModelsHypothesis Tests with Monotonicity ConstraintsHypothesis Tests with Dependent Variable TransformationsHypothesis Tests with One-Way ANOVAUsing the DESIGN Output OptionDiscrete Choice Experiments: DESIGN, NORESTORE, NOZEROCenteringDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
In this example, the data are from an experiment in which nitrogen oxide emissions from a single cylinder engine are measured
for various combinations of fuel, compression ratio, and equivalence ratio. The data are provided by Brinkman (1981). This gas data set is available from the Sashelp library.
The equivalence ratio and nitrogen oxide variables are continuous and numeric, so spline transformations of these variables
are requested. The spline transformation of the dependent variable is restricted to be monotonic. Each spline is degree three
with nine knots (one at each decile) in order to give PROC TRANSREG a great deal of freedom in finding transformations. The
compression ratio variable has only five discrete values, so an optimal scoring is requested with monotonicity constraints.
The character variable Fuel is nominal, so it is optimally scored without any monotonicity constraints. Observations with missing values are excluded
with the NOMISS
a-option.
ods graphics on;
title 'Gasoline Example';
title2 'Iteratively Estimate NOx, CpRatio, EqRatio, and Fuel';
* Fit the Nonparametric Model;
proc transreg data=sashelp.Gas solve test nomiss plots=all;
ods exclude where=(_path_ ? 'MV');
model mspline(NOx / nknots=9) = spline(EqRatio / nknots=9)
monotone(CpRatio) opscore(Fuel);
run;
Output 104.1.1: Transformation Regression Example: The Nonparametric Model
| TRANSREG MORALS Algorithm Iteration History for Mspline(NOx) | |||||
|---|---|---|---|---|---|
| Iteration Number |
Average Change |
Maximum Change |
R-Square | Criterion Change |
Note |
| 0 | 0.41900 | 3.80550 | 0.05241 | ||
| 1 | 0.11984 | 0.83327 | 0.91028 | 0.85787 | |
| 2 | 0.03727 | 0.17688 | 0.93981 | 0.02953 | |
| 3 | 0.02795 | 0.10880 | 0.94969 | 0.00987 | |
| 4 | 0.02088 | 0.07279 | 0.95382 | 0.00413 | |
| 5 | 0.01530 | 0.05031 | 0.95582 | 0.00201 | |
| 6 | 0.01130 | 0.03922 | 0.95688 | 0.00106 | |
| 7 | 0.00852 | 0.03197 | 0.95748 | 0.00060 | |
| 8 | 0.00657 | 0.02531 | 0.95783 | 0.00035 | |
| 9 | 0.00510 | 0.01975 | 0.95805 | 0.00022 | |
| 10 | 0.00398 | 0.01534 | 0.95818 | 0.00013 | |
| 11 | 0.00314 | 0.01200 | 0.95827 | 0.00009 | |
| 12 | 0.00250 | 0.00953 | 0.95832 | 0.00005 | |
| 13 | 0.00199 | 0.00752 | 0.95836 | 0.00003 | |
| 14 | 0.00159 | 0.00594 | 0.95838 | 0.00002 | |
| 15 | 0.00127 | 0.00470 | 0.95839 | 0.00001 | |
| 16 | 0.00102 | 0.00373 | 0.95840 | 0.00001 | |
| 17 | 0.00081 | 0.00297 | 0.95841 | 0.00001 | |
| 18 | 0.00065 | 0.00237 | 0.95841 | 0.00000 | |
| 19 | 0.00052 | 0.00189 | 0.95841 | 0.00000 | |
| 20 | 0.00042 | 0.00151 | 0.95842 | 0.00000 | |
| 21 | 0.00033 | 0.00120 | 0.95842 | 0.00000 | |
| 22 | 0.00027 | 0.00096 | 0.95842 | 0.00000 | |
| 23 | 0.00021 | 0.00077 | 0.95842 | 0.00000 | |
| 24 | 0.00017 | 0.00061 | 0.95842 | 0.00000 | |
| 25 | 0.00014 | 0.00049 | 0.95842 | 0.00000 | |
| 26 | 0.00011 | 0.00039 | 0.95842 | 0.00000 | |
| 27 | 0.00009 | 0.00031 | 0.95842 | 0.00000 | |
| 28 | 0.00007 | 0.00025 | 0.95842 | 0.00000 | |
| 29 | 0.00006 | 0.00020 | 0.95842 | 0.00000 | |
| 30 | 0.00005 | 0.00016 | 0.95842 | 0.00000 | Not Converged |
| The TRANSREG Procedure Hypothesis Tests for Mspline(NOx) Nitrogen Oxide |
| Univariate ANOVA Table Based on the Usual Degrees of Freedom | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares | Mean Square | F Value | Liberal p |
| Model | 21 | 326.0176 | 15.52465 | 161.35 | >= <.0001 |
| Error | 147 | 14.1443 | 0.09622 | ||
| Corrected Total | 168 | 340.1619 | |||
| The above statistics are not adjusted for the fact that the dependent variable was transformed and so are generally liberal. | |||||
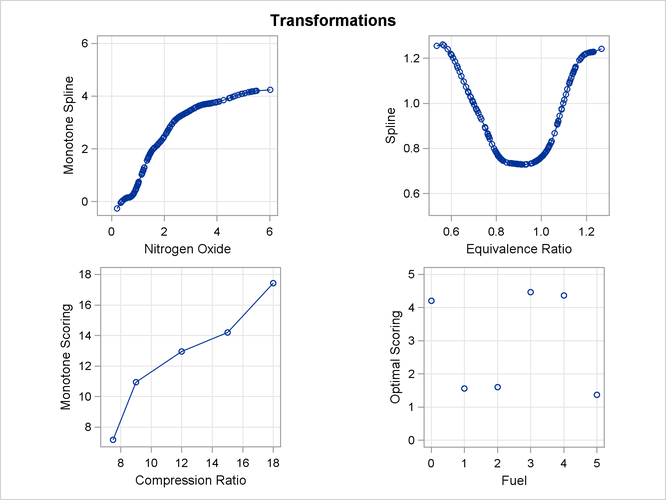

The squared multiple correlation for the initial model is approximately 0.05. PROC TRANSREG increases the R square to over
0.95 by transforming the variables. The transformation plots show how each variable is transformed. The transformation of
compression ratio (TCpRatio) is nearly linear. The transformation of equivalence ratio (TEqRatio) is nearly parabolic. It can be seen from this plot that the optimal transformation of equivalence ratio is nearly uncorrelated
with the original scoring. This suggests that the large increase in R square is due to this transformation. The transformation
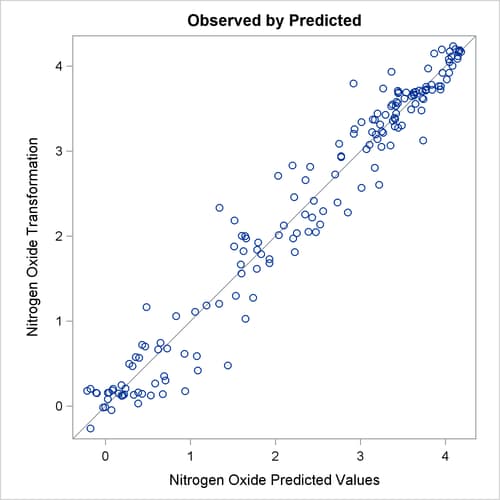
of nitrogen oxide (TNOx) is similar to a log transformation. The final plot shows the transformed dependent variable plotted as a function of the
predicted values. This plot is reasonably linear, showing that the nonlinearities in the data are being accounted for fairly
well by the TRANSREG model.
These results suggest the parametric model
![\begin{eqnarray*} \log (\mbox{NOX}) & = & b_0 + b_1 \times \Variable{EqRatio} + b_2 \times \Variable{EqRatio}^2 + b_3 \times \Variable{CpRatio} \\[0.10in]& & ~ + \sum _ j b_ j \mbox{class}_ j (\Variable{Fuel}) + \mbox{error} \\ \end{eqnarray*}](images/statug_transreg0148.png)
You can perform this analysis with PROC TRANSREG. The following statements produce Output 104.1.2:
title2 'Now fit log(NOx) = b0 + b1*EqRatio + b2*EqRatio**2 +';
title3 'b3*CpRatio + Sum b(j)*Fuel(j) + Error';
*-Fit the Parametric Model Suggested by the Nonparametric Analysis-;
proc transreg data=sashelp.Gas solve ss2 short nomiss plots=all;
model log(NOx) = pspline(EqRatio / deg=2) identity(CpRatio)
opscore(Fuel);
run;
Output 104.1.2: Transformation Regression Example: The Parametric Model
| Univariate Regression Table Based on the Usual Degrees of Freedom | |||||||
|---|---|---|---|---|---|---|---|
| Variable | DF | Coefficient | Type II Sum of Squares |
Mean Square | F Value | Pr > F | Label |
| Intercept | 1 | -15.274649 | 57.1338 | 57.1338 | 1227.60 | <.0001 | Intercept |
| Pspline.EqRatio_1 | 1 | 35.102914 | 62.7478 | 62.7478 | 1348.22 | <.0001 | Equivalence Ratio 1 |
| Pspline.EqRatio_2 | 1 | -19.386468 | 64.6430 | 64.6430 | 1388.94 | <.0001 | Equivalence Ratio 2 |
| Identity(CpRatio) | 1 | 0.032058 | 1.4445 | 1.4445 | 31.04 | <.0001 | Compression Ratio |
| Opscore(Fuel) | 5 | 0.158388 | 5.5619 | 1.1124 | 23.90 | <.0001 | Fuel |
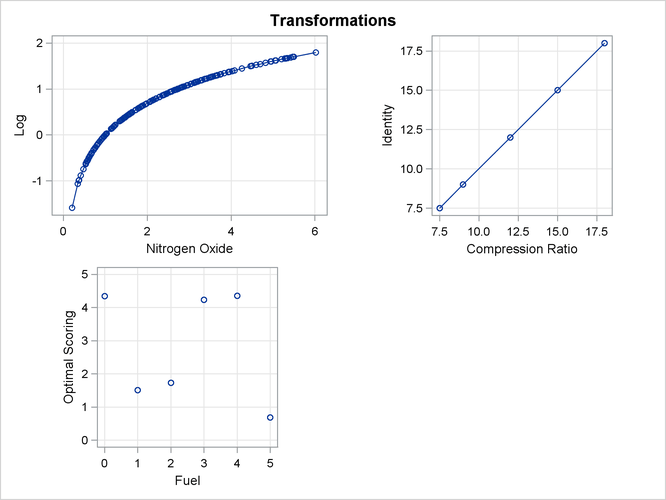

The LOG
transformation computes the natural log. The PSPLINE
expansion expands EqRatio into a linear term, EqRatio, and a squared term, ![]() . An identity transformation of
. An identity transformation of CpRatio and an optimal scoring of Fuel is requested. These should provide a good parametric operationalization of the optimal transformations. The final model has
an R square of 0.91 (smaller than before since the model has fewer parameters, but still quite good).