The NPAR1WAY Procedure

Fligner-Policello Test

If you specify the FP option, PROC NPAR1WAY computes the Fligner-Policello location test for two-sample data (Fligner and Policello, 1981). The null hypothesis for the test is $H_0: \theta _ X = \theta _ Y$ , where $\theta _ X$ and $\theta _ Y$ are the population medians of the two classes. The Fligner-Policello test assumes that the distribution in each class is symmetric around the class median, but it does not require that the two class distributions have the same form or that the class variances be equal. For more information, see Hollander and Wolfe (1999) and Juneau (2007).

The Fligner-Policello test is based on placement scores (Orban and Wolfe, 1979). The placement of an observation $X_ i$ from class X, $P(X_ i)$ , is defined as the number of observations in class Y that are less than $X_ i$ . If there are ties, the placement of $X_ i$ is adjusted by adding half the number of observations in class Y that are equal to $X_ i$ . The placement of an observation $Y_ j$ from class Y, $P(Y_ j)$ , is defined in the same way. The placements can be expressed as

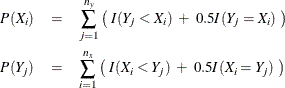
$\begin{eqnarray*} P(X_ i) & = & \sum _{j=1}^{n_ y} \left( ~ I( Y_ j < X_ i ) ~ + ~ 0.5 I( Y_ j = X_ i) ~ \right) \\ P(Y_ j) & = & \sum _{i=1}^{n_ x} \left( ~ I( X_ i < Y_ j ) ~ + ~ 0.5 I( X_ i = Y_ j) ~ \right) \end{eqnarray*}$

where $I(\cdot )$ is an indicator function and $n_ x$ and $n_ y$ denote the number of observations in class X and class Y, respectively.

The average placements for class X and class Y are computed as

$\begin{eqnarray*} \bar{P}_ x & = & \left( \sum _{i=1}^{n_ x} P(X_ i) \right) ~ / ~ n_ x \\[0.05in] \bar{P}_ y & = & \left( \sum _{j=1}^{n_ y} P(Y_ j) \right) ~ / ~ n_ y \end{eqnarray*}$

The Fligner-Policello test statistic is computed as

$z = \left( \sum _{j=1}^{n_ y} P(Y_ j) - \sum _{i=1}^{n_ x} P(X_ i) \right) ~ / ~ \left( 2 \sqrt { V_ x + V_ y + \bar{P}_ x \bar{P}_ y } \right)$

where

$\begin{eqnarray*} V_ x & = & \sum _{i=1}^{n_ x} (P(X_ i) - \bar{P}_ x)^2 \\[0.05in] V_ y & = & \sum _{j=1}^{n_ y} (P(Y_ j) - \bar{P}_ y)^2 \end{eqnarray*}$

and the standard deviation of the placements is $\sqrt {V_ x / (n_ x-1)}$ for class X and $\sqrt {V_ y / (n_ y-1)}$ for class Y.

Under the null hypothesis, the Fligner-Policello statistic has an asymptotic standard normal distribution. PROC NPAR1WAY provides one- and two-sided asymptotic p-values for the Fligner-Policello test. For the one-sided test, PROC NPAR1WAY displays the right-sided p-value when the test statistic z is greater than its null hypothesis expected value of zero. PROC NPAR1WAY displays the left-sided p-value when the test statistic z is less than or equal to zero. The one-sided p-value $P_1(z)$ can be expressed as

$\begin{equation*} P_1(z) = \begin{cases} \mr{Prob} (Z > z) \quad \mr{if} \hspace{.1in} z > 0 \\ \mr{Prob} (Z < z) \quad \mr{if} \hspace{.1in} z \leq 0 \\ \end{cases}\end{equation*}$

where Z has a standard normal distribution. The two-sided p-value $P_{2}(z)$ is computed as Prob(|Z| > |z|).

When you specify the FP option, PROC NPAR1WAY displays a "Fligner-Policello Placements" table and a "Fligner-Policello Test" table. The "Fligner-Policello Placements" table contains the following information for each of the two classes: number of observations, sum of the placements, average placement, and standard deviation of the placements. The "Fligner-Policello Test" table contains the test statistic z and the corresponding one- and two-sided p-values. This table also displays the difference between the class placement sums, which is the numerator of the test statistic. When ODS Graphics is enabled and you specify the FP or PLOTS=FPBOXPLOT option, PROC NPAR1WAY provides a box plot of the Fligner-Policello placements.

PROC NPAR1WAY computes the Fligner-Policello difference (the numerator of the test statistic) as the placement sum for class Y minus the placement sum for class X (the reference class). By default, PROC NPAR1WAY uses the first class that is listed in the "Fligner-Policello Placements" table as class Y and the second class as the reference class X. The table displays class levels in the order in which they appear in the input data set. To use the first class (instead of the second class) as the reference class for the Fligner-Policello test, you can specify the FP(REFCLASS=1) option. Or you can specify the FP(REFCLASS=class-value) option to identify the reference class by the formatted value of the CLASS variable.