-
ALPHA=

-
specifies the level of significance  used in the construction of
used in the construction of 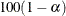 % confidence intervals. The value must be strictly between 0 and 1; the default value of
% confidence intervals. The value must be strictly between 0 and 1; the default value of 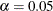 results in 95% intervals. This value is used as the default confidence level for limits computed in the "Parameter Estimates"
table and with the LCLM
, LCL
, UCLM
, and UCL
options in the OUTPUT
statement.
results in 95% intervals. This value is used as the default confidence level for limits computed in the "Parameter Estimates"
table and with the LCLM
, LCL
, UCLM
, and UCL
options in the OUTPUT
statement.
-
BEST=n
-
requests that PROC NLIN display the residual sums of squares only for the best n combinations of possible starting values from the grid. If you do not specify the BEST= option, PROC NLIN displays the residual
sum of squares for every combination of possible parameter starting values.
-
BIAS
-
adds Box’s bias and percentage bias measures to the "Parameter Estimates" table (Box, 1971). Box’s bias measure, along with Hougaard’s measure of skewness, is used for assessing a parameter estimator’s close-to-linear
behavior (Ratkowsky, 1983, 1990). Hence, it is useful for identifying problematic parameters (Seber and Wild, 1989, sec. 4.7.1). When you specify the BIAS option, Box’s bias measure (Box, 1971) and the percentage bias (the bias expressed as a percentage of the least-squares estimator) are added for each parameter
to the "Parameter Estimates" table. Ratkowsky (1983, p. 21) takes a percentage bias in excess of 1% to be a good rule of thumb for indicating nonlinear behavior.
See the section Box’s Measure of Bias for further details. Example 69.4 shows how to use this measure, along with Hougaard’s measure of skewness, to evaluate changes in the parameterization of
a nonlinear model. Computation of the Box’s bias measure requires first and second derivatives. If you do not provide derivatives
with the DER
statement—and it is recommended that you do not—the analytic derivatives are computed for you.
-
CONVERGE=c
-
specifies the convergence criterion for PROC NLIN. For all iterative methods the relative offset convergence measure of Bates and Watts is used by default to determine convergence.
This measure is labeled "R" in the "Estimation Summary" table. The iterations are said to have converged for CONVERGE=c if
where  is the residual vector and
is the residual vector and 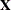 is the
is the 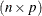 matrix of first derivatives with respect to the parameters. The default LOSS function is the sum of squared errors (SSE),
and
matrix of first derivatives with respect to the parameters. The default LOSS function is the sum of squared errors (SSE),
and 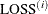 denotes the value of the loss function at the ith iteration. By default, CONVERGE=
denotes the value of the loss function at the ith iteration. By default, CONVERGE=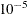 . The R convergence measure cannot be computed accurately in the special case of a perfect fit (residuals close to zero).
When the SSE is less than the value of the SINGULAR=
criterion, convergence is assumed.
. The R convergence measure cannot be computed accurately in the special case of a perfect fit (residuals close to zero).
When the SSE is less than the value of the SINGULAR=
criterion, convergence is assumed.
-
CONVERGEOBJ=c
-
uses the change in the LOSS function as the convergence criterion and tunes the criterion. The iterations are said to have
converged for CONVERGEOBJ=c if
where LOSS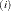 is the LOSS for the ith iteration. The default LOSS function is the sum of squared errors (SSE), the residual sum of squares. The constant c should be a small positive number. For more details about the LOSS function, see the section Special Variable Used to Determine Convergence Criteria. For more details about the computational methods in the NLIN procedure, see the section Computational Methods.
is the LOSS for the ith iteration. The default LOSS function is the sum of squared errors (SSE), the residual sum of squares. The constant c should be a small positive number. For more details about the LOSS function, see the section Special Variable Used to Determine Convergence Criteria. For more details about the computational methods in the NLIN procedure, see the section Computational Methods.
Note that in SAS 6 the CONVERGE=
and CONVERGEOBJ= options both requested that convergence be tracked by the relative change in the loss function. If you specify
the CONVERGEOBJ= option in newer releases, the CONVERGE= option is disabled. This enables you to track convergence as in SAS
6.
-
CONVERGEPARM=c
-
uses the maximum change among parameter estimates as the convergence criterion and tunes the criterion. The iterations are
said to have converged for CONVERGEPARM=c if
where 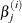 is the value of the jth parameter at the ith iteration.
is the value of the jth parameter at the ith iteration.
The default convergence criterion is CONVERGE
. If you specify CONVERGEPARM=c, the maximum change in parameters is used as the convergence criterion. If you specify both the CONVERGEOBJ=
and CONVERGEPARM= options, PROC NLIN continues to iterate until the decrease in LOSS is sufficiently small (as determined
by the CONVERGEOBJ=
option) and the maximum change among the parameters is sufficiently small (as determined by the CONVERGEPARM= option).
-
DATA=SAS-data-set
-
specifies the input SAS data set to be analyzed by PROC NLIN. If you omit the DATA= option, the most recently created SAS
data set is used.
-
FLOW
-
displays a message for each statement in the model program as it is executed. This debugging option is rarely needed, and it produces large amounts of output.
-
G4
-
uses a Moore-Penrose inverse (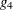 -inverse) in parameter estimation. See Kennedy and Gentle (1980) for details.
-inverse) in parameter estimation. See Kennedy and Gentle (1980) for details.
-
HOUGAARD
-
adds Hougaard’s measure of skewness to the "Parameter Estimates" table (Hougaard, 1982, 1985). The skewness measure is one method of assessing a parameter estimator’s close-to-linear behavior in the sense of Ratkowsky
(1983, 1990). The behavior of estimators that are close to linear approaches that of least squares estimators in linear models, which
are unbiased and have minimum variance. When you specify the HOUGAARD option, the standardized skewness measure of Hougaard
(1985) is added for each parameter to the "Parameter Estimates" table. Because of the linkage between nonlinear behavior of a parameter
estimator in nonlinear regression and the nonnormality of the estimator’s sampling distribution, Ratkowsky (1990, p. 28) provides the following rules to interpret the (standardized) Hougaard skewness measure:
-
Values less than 0.1 in absolute value indicate very close-to-linear behavior.
-
Values between 0.1 and 0.25 in absolute value indicate reasonably close-to-linear behavior.
-
The nonlinear behavior is apparent for absolute values above 0.25 and is considerable for absolute values above 1.
See the section Hougaard’s Measure of Skewness for further details. Example 69.4 shows how to use this measure to evaluate changes in the parameterization of a nonlinear model. Computation of the Hougaard
skewness measure requires first and second derivatives. If you do not provide derivatives with the DER
statement—and it is recommended that you do not—the analytic derivatives are computed for you. For weighted least squares,
the NLIN procedure ignores the weights for computing the Hougaard skewness measure. This can be a strong assumption as the
formulation in Hougaard (1985) assumes homoscedastic errors.
-
LIST
-
displays the model program and variable lists, including the statements added by macros. Note that the expressions displayed
by the LIST option do not necessarily represent the way the expression is actually calculated—because intermediate results
for common subexpressions can be reused—but are shown in expanded form. To see how the expression is actually evaluated, use
the LISTCODE
option.
-
LISTALL
-
selects the LIST
, LISTDEP
, LISTDER
, and LISTCODE
options.
-
LISTCODE
-
displays the derivative tables and the compiled model program code. The LISTCODE option is a debugging feature and is not
normally needed.
-
LISTDEP
-
produces a report that lists, for each variable in the model program, the variables that depend on it and the variables on
which it depends.
-
LISTDER
-
displays a table of derivatives. The derivatives table lists each nonzero derivative computed for the problem. The derivative
listed can be a constant, a variable in the model program, or a special derivative variable created to hold the result of
an expression.
-
MAXITER=n
-
specifies the maximum number n of iterations in the optimization process. The default is n = 100.
-
MAXSUBIT=n
-
places a limit on the number of step halvings. The value of MAXSUBIT must be a positive integer and the default value is n = 30.
-
METHOD=GAUSS | MARQUARDT | NEWTON | GRADIENT
-
specifies the iterative method employed by the NLIN procedure in solving the nonlinear least squares problem. The GAUSS, MARQUARDT,
and NEWTON methods are more robust than the GRADIENT method. If you omit the METHOD= option, METHOD=GAUSS is used. See the
section Computational Methods for more information.
-
NLINMEASURES
-
displays the global nonlinearity measures table. These measures include the maximum intrinsic and parameter-effects curvatures
(Bates and Watts, 1980), the root mean square (RMS) intrinsic and parameter-effects curvatures and the critical curvature value (Bates and Watts,
1980). In addition, the variances of the ordinary and projected residuals are included. According to Bates and Watts (1980), both intrinsic and parameter-effects curvatures are deemed negligible if they are less than the critical curvature value.
This critical value is given by 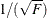 where
where 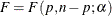 . The value
. The value 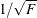 can be considered as the radius of curvature of the
can be considered as the radius of curvature of the 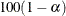 percent confidence region (Bates and Watts, 1980). For weighted least squares, the NLIN procedure ignores the weights for computing the curvature measures. This can be a
strong assumption as the original derivation in Bates and Watts (1980) assumes homoscedastic errors.
percent confidence region (Bates and Watts, 1980). For weighted least squares, the NLIN procedure ignores the weights for computing the curvature measures. This can be a
strong assumption as the original derivation in Bates and Watts (1980) assumes homoscedastic errors.
-
NOITPRINT
-
suppresses the display of the "Iteration History" table.
-
NOHALVE
-
removes the restriction that the objective value must decrease at every iteration. Step halving is still used to satisfy BOUNDS
and to ensure that the number of observations that can be evaluated does not decrease. The NOHALVE option can be useful in
weighted nonlinear least squares problems where the weights depend on the parameters, such as in iteratively reweighted least
squares (IRLS) fitting. See Example 69.2 for an application of IRLS fitting.
-
NOPRINT
-
suppresses the display of the output. Note that this option temporarily disables the Output Delivery System (ODS). For more
information, see Chapter 20: Using the Output Delivery System.
-
OUTEST=SAS-data-set
-
specifies an output data set that contains the parameter estimates produced at each iteration. See the section Output Data Sets for details. If you want to create a SAS data set in a permanent library, you must specify a two-level name. For more information
about permanent libraries and SAS data sets, see
SAS Language Reference: Concepts.
-
PLOTS <(global-plot-option)> <= (plot-request<(options)> <... plot-request<(options)>>)>
-
controls most of the plots that are produced through ODS Graphics (other plots are controlled by the BOOTSTRAP
and PROFILE
statements). When you specify only one plot-request, you can omit the parentheses around it. Here are some examples:
plots
plots = none
plots = diagnostics(unpack)
plots = fit(stats=none)
plots = residuals(residualtype=proj unpack smooth)
plots(stats=all) = (diagnostics(stats=(maxincurv maxpecurv)) fit)
ODS Graphics must be enabled before plots can be requested. For example:
ods graphics on;
proc nlin plots=diagnostics(stats=all);
model y = alpha - beta*(gamma**x);
run;
ods graphics off;
For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.
If ODS Graphics is enabled and if you specify the PLOTS option without any global-plot-option or plot-requests, PROC NLIN produces the plots listed in Table 69.2 with the default set of statistics and options. If you do not specify the PLOTS option, PROC NLIN does not produce any of
these graphs.
Table 69.2: Graphs Produced When the PLOTS Option Is Specified
|
Plot
|
Conditional On
|
|
ContourFitPlot
|
Model with two regressors
|
|
FitDiagnosticsPanel
|
Unconditional
|
|
FitPlot
|
Model with one regressor
|
|
LeveragePlot
|
Unconditional
|
|
LocalInfluencePlot
|
Unconditional
|
|
ResidualPanel
|
Unconditional
|
You can request additional plots by specifying plot-requests. For a listing of all the plots that PROC NLIN produces, see the section ODS Graphics. Each global-plot-option applies to all plots that are generated by the NLIN procedure except for plots that are controlled by the BOOTSTRAP
and PROFILE
statements. The global-plot-option can be overridden by a specific option after a plot-request.
The following global-plot-options are available:
-
RESIDUALTYPE=RAW | PROJ | BOTH
-
specifies the residual type to be plotted in the fit diagnostics and residual plots. RESIDUALTYPE=RAW requests that only the
ordinary residuals be included in the plots; RESIDUALTYPE=PROJ sets the choice to projected residuals. By default, both residual
types are included, which can also be effected by setting RESIDUALTYPE=BOTH. See the section Residuals in Nonlinear Regression for details about the properties of ordinary and projected residuals in nonlinear regression.
-
STATS=ALL | DEFAULT | NONE | (plot-statistics)
-
requests the statistics to be included in all plots, except the ResidualPlots and the unpacked diagnostics plots. Table 69.3 lists the statistics that you can request. STATS=ALL requests all these statistics, STATS=NONE suppresses all statistics,
and STATS=DEFAULT selects the default statistics. You request statistics in addition to the default set by including the keyword
DEFAULT in the plot-statistics list.
Table 69.3: Statistics Available in Plots
|
Keyword
|
Default
|
Description
|
|
DEFAULT
|
|
All default statistics
|
|
MAXINCURV
|
|
Maximum intrinsic curvature
|
|
MAXPECURV
|
|
Maximum parameter-effects curvature
|
|
MSE
|
x
|
Mean squared error, estimated or set by the SIGSQ
option
|
|
NOBS
|
x
|
Number of observations used
|
|
NPARM
|
x
|
Number of parameters in the model
|
|
PVAR
|
x
|
Estimated variance of the projected residuals
|
|
RMSINCURV
|
|
Root mean square intrinsic curvature
|
|
RMSPECURV
|
|
Root mean square parameter-effects curvature
|
|
VAR
|
x
|
Estimated variance of the ordinary residuals
|
Along with the maximum intrinsic and parameter-effects curvatures, the critical curvature (CURVCRIT) value, 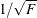 where
where 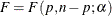 , is also displayed. You do not need to specify any option for it. See the section Relative Curvature Measures of Nonlinearity for details about curvature measures of nonlinearity.
, is also displayed. You do not need to specify any option for it. See the section Relative Curvature Measures of Nonlinearity for details about curvature measures of nonlinearity.
-
UNPACK
-
suppresses paneling.
You can specify the following plot-requests in the PLOTS= option:
-
ALL
-
produces all appropriate plots.
-
NONE
-
suppresses all plots.
-
DIAGNOSTICS <(diagnostics-options)>
-
produces a summary panel of fit diagnostics, leverage plots, and local-influence plots. The fit diagnostics panel includes:
-
histogram of the ordinary residuals
-
histogram of the projected residuals
-
response variable values versus the predicted values
-
expectation or mean of the ordinary residuals versus the predicted values
-
ordinary and projected residuals versus the predicted values
-
standardized ordinary and projected residuals versus the predicted values
-
standardized ordinary and projected residuals versus the tangential leverage
-
standardized ordinary and projected residuals versus the Jacobian leverage
-
box plot of the ordinary and projected residuals if you specify the STATS=NONE suboption
The leverage and local influence plots are produced separately. The leverage plot is an index plot of the tangential and
Jacobian leverages (by observation), and the local-influence plot contains the local influence by observation for a perturbation
of the response variable. See the sections Leverage in Nonlinear Regression and Local Influence in Nonlinear Regression for a some details about leverages and local-influence in nonlinear regression.
You can specify the following diagnostics-options:
-
RESIDUALTYPE=RAW | PROJ | BOTH
-
specifies the residual type to be plotted in the panel. See the RESIDUALTYPE= global-plot-option for details. This diagnostics-option overrides the PLOTS RESIDUALTYPE global-plot-option. Only the plots that overlay both ordinary and projected residuals in the same plot are affected by this option.
-
LEVERAGETYPE=TAN | JAC | BOTH
-
specifies the leverage type to be plotted in the leverage plot. LEVERAGETYPE=TAN specifies that only the tangential leverage
be included in the leverage plot, and LEVERAGETYPE=JAC specifies that only the Jacobian leverage be included. By default,
both are displayed in the leverage plot. The same result can be effected by setting LEVERAGETYPE=BOTH. Only the leverage plot
is affected by this option.
-
LABELOBS
-
specifies that the leverage and local-influence plots be labeled with the observation number. Only these two plots are affected
by this option.
-
STATS=stats-options
-
determines which statistics are included in the panel. See the STATS= global-plot-option for details. This diagnostics-option overrides the PLOTS STATS global-plot-option.
-
UNPACK
-
produces the plots in the diagnostics panel as individual plots. The statistics panel is not included in the individual plots,
even if STATS= global-plot-option or STATS= diagnostics-option or both are specified.
-
FITPLOT | FIT <(fit-options)>
-
produces, depending on the number of regressors, a scatter or contour fit plot. For a single-regressor model, a scatter plot
of the data overlaid with the regression curve, confidence, and prediction bands is produced. For two-regressor models, a
contour fit plot of the model with overlaid data is produced. If the model contains more than two regressors, no fit plot
is produced.
You can specify the following fit-options:
-
NOCLI
-
suppresses the prediction limits for single-regressor models.
-
NOCLM
-
suppresses the confidence limits for single-regressor models.
-
NOLIMITS
-
suppresses the confidence and prediction limits for single-regressor models.
-
OBS=GRADIENT | NONE | OUTLINE | OUTLINEGRADIENT
-
controls how the observations are displayed. The suboptions are as follows:
- GRADIENT
-
specifies that observations be displayed as circles colored by the observed response. The same color gradient is used to display
the fitted surface and the observations. Observations for which the predicted response is close to the observed response have
similar colors—the greater the contrast between the color of an observation and the surface, the larger the residual is at
that point. OBS=GRADIENT is the default.
- NONE
-
suppresses the observations.
- OUTLINE
-
specifies that observations be displayed as circles with a border but with a completely transparent fill.
- OUTLINEGRADIENT
-
is the same as OBS=GRADIENT except that a border is shown around each observation. This option is useful for identifying the
location observations for which the residuals are small, because at these points the color of the observations and the color
of the surface are indistinguishable.
-
CONTLEG
-
specifies that a continuous legend be included in the contour fit plot of a two-regressor model.
-
STATS=stats-options
-
determines which model fit statistics are included in the panel. See the STATS= global-plot-option for details. This fit-option overrides the PLOTS STATS global-plot-option.
-
RESIDUALS <(residual-options)>
-
produces panels of the ordinary and projected residuals versus the regressors in the model. Each panel contains at most six
plots, and multiple panels are used in the case where there are more than six regressors in the model.
The following residual-options are available:
-
RESIDUALTYPE=RAW | PROJ | BOTH
-
specifies the residual type to be plotted in the panel. See the RESIDUALTYPE= global-plot-option for details. This residual-option overrides the PLOTS RESIDUALTYPE global-plot-option.
-
SMOOTH
-
requests a nonparametric smooth of the residuals for each regressor. Each nonparametric fit is a loess fit that uses local
linear polynomials, linear interpolation, and a smoothing parameter selected that yields a local minimum of the corrected
Akaike information criterion (AICC). See Chapter 59: The LOESS Procedure, for details.
-
UNPACK
-
suppresses paneling.
-
PRINT
-
displays the result of each statement in the program as it is executed. This option is a debugging feature that produces large
amounts of output and is normally not needed.
-
RHO=value
-
specifies a value that controls the step-size search. By default RHO=0.1, except when METHOD=
MARQUARDT. In that case, RHO=10. See the section Step-Size Search for more details.
-
SAVE
-
specifies that, when the iteration limit is exceeded, the parameter estimates from the final iteration be output to the OUTEST=
data set. These parameter estimates are associated with the observation for which _TYPE_="FINAL". If you omit the SAVE option, the parameter estimates from the final iteration are not output to the data set unless
convergence has been attained.
-
SIGSQ=value
-
specifies a value to use as the estimate of the residual variance in lieu of the estimated mean-squared error. This value
is used in computing the standard errors of the estimates. Fixing the value of the residual variance can be useful, for example,
in maximum likelihood estimation.
-
SINGULAR=s
-
specifies the singularity criterion, s, which is the absolute magnitude of the smallest pivot value allowed when inverting the Hessian or the approximation to the
Hessian. The default value is 1E4 times the machine epsilon; this product is approximately 1E-12 on most computers.
-
SMETHOD=HALVE | GOLDEN | CUBIC
-
specifies the step-size search method. The default is SMETHOD=HALVE. See the section Step-Size Search for details.
-
TAU=value
-
specifies a value that is used to control the step-size search. The default is TAU=1, except when METHOD=
MARQUARDT. In that case the default is TAU=0.01. See the section Step-Size Search for details.
-
TOTALSS
-
adds to the analysis of variance table the uncorrected total sum of squares in models that have an (implied) intercept, and
adds the corrected total sum of squares in models that do not have an (implied) intercept.
-
TRACE
-
displays the result of each operation in each statement in the model program as it is executed, in addition to the information
displayed by the FLOW
and PRINT
options. This debugging option is needed very rarely, and it produces even more output than the FLOW
and PRINT
options.
-
XREF
-
displays a cross-reference of the variables in the model program showing where each variable is referenced or given a value.
The XREF listing does not include derivative variables.
-
UNCORRECTEDDF
-
specifies that no degrees of freedom be lost when a bound is active. When the UNCORRECTEDDF option is not specified, an active
bound is treated as if a restriction were applied to the set of parameters, so one parameter degree of freedom is deducted.


 Automatic DerivativesMeasures of Nonlinearity, Diagnostics and InferenceMissing ValuesSpecial VariablesTroubleshootingComputational MethodsOutput Data SetsConfidence IntervalsCovariance Matrix of Parameter EstimatesConvergence MeasuresDisplayed OutputIncompatibilities with SAS 6.11 and Earlier Versions of PROC NLINODS Table NamesODS Graphics
Automatic DerivativesMeasures of Nonlinearity, Diagnostics and InferenceMissing ValuesSpecial VariablesTroubleshootingComputational MethodsOutput Data SetsConfidence IntervalsCovariance Matrix of Parameter EstimatesConvergence MeasuresDisplayed OutputIncompatibilities with SAS 6.11 and Earlier Versions of PROC NLINODS Table NamesODS Graphics
![\[ \max _ j \left( \frac{ | \beta _ j^{(i-1)} - \beta _ j^{(i)} | }{ | \beta _ j^{(i-1)} | } \right) < c \]](images/statug_nlin0052.png)