The NLIN Procedure

Example 69.1 Segmented Model

Suppose you are interested in fitting a model that consists of two segments that connect in a smooth fashion. For example, the following model states that for values of x less than $x_0$ the mean of Y is a quadratic function in x, and for values of x greater than $x_0$ the mean of Y is constant:

$\mr{E}[Y|x] = \left\{ \begin{array}{ll} \alpha + \beta x + \gamma x^2 & \quad \mr{if} \, \, \, x < x_0 \cr c & \quad \mr{if} \, \, \, x \ge x_0 \end{array} \right.$

In this model equation $\alpha$ , $\beta$ , and $\gamma$ are the coefficients of the quadratic segment, and c is the plateau of the mean function. The NLIN procedure can fit such a segmented model even when the join point, $x_0$ , is unknown.

We also want to impose conditions on the two segments of the model. First, the curve should be continuous—that is, the quadratic and the plateau section need to meet at $x_0$ . Second, the curve should be smooth—that is, the first derivative of the two segments with respect to x need to coincide at $x_0$ .

The continuity condition requires that

$p = \mr{E}[Y|x_0] = \alpha + \beta x_0 + \gamma x_0^2$

The smoothness condition requires that

$\frac{\partial \mr{E}[Y|x_0]}{\partial x} = \beta + 2\gamma x_0 \equiv 0$

If you solve for $x_0$ and substitute into the expression for c, the two conditions jointly imply that

$\begin{align*} x_0 & = - \beta / 2 \gamma \\ c & = \alpha - \beta ^2 / 4 \gamma \\ \end{align*}$

Although there are apparently four unknowns, the model contains only three parameters. The continuity and smoothness restrictions together completely determine one parameter given the other three.

The following DATA step creates the SAS data set for this example:

data a;
   input y x @@;
   datalines;
.46 1  .47  2 .57  3 .61  4 .62  5 .68  6 .69  7
.78 8  .70  9 .74 10 .77 11 .78 12 .74 13 .80 13
.80 15 .78 16
;

The following PROC NLIN statements fit this segmented model:

title 'Quadratic Model with Plateau';
proc nlin data=a;
   parms alpha=.45 beta=.05 gamma=-.0025;

   x0 = -.5*beta / gamma;

   if (x < x0) then
        mean = alpha + beta*x  + gamma*x*x;
   else mean = alpha + beta*x0 + gamma*x0*x0;
   model y = mean;

   if _obs_=1 and _iter_ =.  then do;
      plateau =alpha + beta*x0 + gamma*x0*x0;
      put /  x0= plateau=  ;
   end;
   output out=b predicted=yp;
run;

The parameters of the model are $\alpha$ , $\beta$ , and $\gamma$ , respectively. They are represented in the PROC NLIN statements by the variables alpha, beta, and gamma, respectively. In order to model the two segments, a conditional statement is used that assigns the appropriate expression to the mean function depending on the value of $x_0$ . A PUT statement is used to print the constrained parameters every time the program is executed for the first observation. The OUTPUT statement computes predicted values for plotting and saves them to data set b.

Note that there are other ways in which you can write the conditional expressions for this model. For example, you could formulate a condition with two model statements, as follows:

proc nlin data=a;
   parms alpha=.45 beta=.05 gamma=-.0025;
   x0 = -.5*beta / gamma;
   if (x < x0) then
        model y = alpha+beta*x+gamma*x*x;
   else model y = alpha+beta*x0+gamma*x0*x0;
run;

Or you could use a single expression with a conditional evaluation, as in the following statements:

proc nlin data=a;
   parms alpha=.45 beta=.05 gamma=-.0025;
   x0 = -.5*beta / gamma;
   model y = (x <x0)*(alpha+beta*x +gamma*x*x) +
             (x>=x0)*(alpha+beta*x0+gamma*x0*x0);
run;

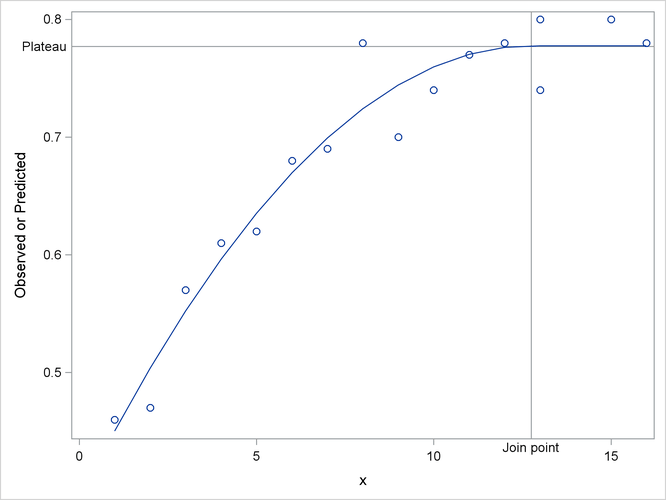
The results from fitting this model with PROC NLIN are shown in Output 69.1.1–Output 69.1.3. The iterative optimization converges after six iterations (Output 69.1.1). Output 69.1.1 indicates that the join point is 12.747 and the plateau value is 0.777.

Output 69.1.1: Nonlinear Least-Squares Iterative Phase

Quadratic Model with Plateau

The NLIN Procedure

Dependent Variable y

Method: Gauss-Newton

Iterative Phase
Iter	alpha	beta	gamma	Sum of Squares
0	0.4500	0.0500	-0.00250	0.0562
1	0.3881	0.0616	-0.00234	0.0118
2	0.3930	0.0601	-0.00234	0.0101
3	0.3922	0.0604	-0.00237	0.0101
4	0.3921	0.0605	-0.00237	0.0101
5	0.3921	0.0605	-0.00237	0.0101
6	0.3921	0.0605	-0.00237	0.0101

NOTE: Convergence criterion met.

Output 69.1.2: Results from Put Statement

x0=12.747669162 plateau=0.7774974276

Output 69.1.3: Least-Squares Analysis for the Quadratic Model

Source	DF	Sum of Squares	Mean Square	F Value	Approx Pr > F
Model	2	0.1769	0.0884	114.22	<.0001
Error	13	0.0101	0.000774
Corrected Total	15	0.1869

Parameter	Estimate	Approx Std Error	Approximate 95% Confidence Limits
alpha	0.3921	0.0267	0.3345	0.4497
beta	0.0605	0.00842	0.0423	0.0787
gamma	-0.00237	0.000551	-0.00356	-0.00118

The following statements produce a graph of the observed and predicted values with reference lines for the join point and plateau estimates (Output 69.1.4):

proc sgplot data=b noautolegend;
   yaxis label='Observed or Predicted';
   refline 0.777  / axis=y label="Plateau"    labelpos=min;
   refline 12.747 / axis=x label="Join point" labelpos=min;
   scatter y=y  x=x;
   series  y=yp x=x;
run;

Output 69.1.4: Observed and Predicted Values for the Quadratic Model

If you want to estimate the join point directly, you can use the relationship between the parameters to change the parameterization of the model in such a way that the mean function depends directly on $x_0$ . Using the smoothness condition that relates $x_0$ to $\gamma$ ,

$x_0 = -\beta /2\gamma$

you can express $\gamma$ as a function of $\beta$ and $x_0$ :

$\gamma = -\beta /(2 x_0)$

Substituting for $\gamma$ in the model equation

$\mr{E}[Y|x] = \left\{ \begin{array}{ll} \alpha + \beta x + \gamma x^2 & \quad \mr{if} \, \, \, x < x_0 \cr \alpha - \beta ^2/(4\gamma ) & \quad \mr{if} \, \, \, x \ge x_0 \end{array} \right.$

yields the reparameterized model

$\mr{E}[Y|x] = \left\{ \begin{array}{ll} \alpha + \beta x (1- x/(2x_0)) & \quad \mr{if} \, \, \, x < x_0 \cr \alpha + \beta x_0 / 2 & \quad \mr{if} \, \, \, x \ge x_0 \end{array} \right.$

This model is fit with the following PROC NLIN statements:

proc nlin data=a;
   parms alpha=.45 beta=.05 x0=10;
   if (x<x0) then
        mean = alpha + beta*x *(1-x/(2*x0));
   else mean = alpha + beta*x0/2;
   model y = mean;
run;

Output 69.1.5: Results from Reparameterized Model

The NLIN Procedure

Dependent Variable y

Method: Gauss-Newton

NOTE: Convergence criterion met.

Source	DF	Sum of Squares	Mean Square	F Value	Approx Pr > F
Model	2	0.1769	0.0884	114.22	<.0001
Error	13	0.0101	0.000774
Corrected Total	15	0.1869

Parameter	Estimate	Approx Std Error	Approximate 95% Confidence Limits
alpha	0.3921	0.0267	0.3345	0.4497
beta	0.0605	0.00842	0.0423	0.0787
x0	12.7477	1.2781	9.9864	15.5089

The analysis of variance table in the reparameterized model is the same as in the earlier analysis (compare Output 69.1.5 and Output 69.1.3). Changing the parameterization of a model does not affect the fit. The "Parameter Estimates" table now shows x0 as a parameter in the model. The estimate agrees with the earlier result that uses the PUT statement (Output 69.1.2). Since $x_0$ is now a model parameter, the NLIN procedure also reports its asymptotic standard error and its approximate 95% confidence interval.